Работа логических элементов: таблица истинности (информатика, 8 класс)
Практически любое цифровое устройство включает в себя логические элементы. На информатике в 8 классе изучают так называемую алгебру логики. Эта наука используется при создании автоматических устройств, аппаратных и информационных вычислительных блоков. По сути, такие элементы реализуют функции сложения, умножения и инверсии дискретного сигнала, являясь преобразователями. Причём их работа поясняется так называемой таблицей истинности.
Оглавление:
Общие сведения
Одним из простых типов данных в информатике считается булевый. Этот примитивный вид может принимать два возможных значения истинный или ложный. В международной системе для описания используются слова true и false. Своё название тип получил благодаря английскому математику Джорджу Буля изучающий логику математических операций. В общем случае под ним понимают действие, соответствующее некому высказыванию. То есть с её помощью получают сложные выражения из простых и используют результат для управления последовательности определённых программ.
Наиболее часто в языках программирования применяется числовой тип описания. В них считается, что ноль соответствует логической лжи, а единица — истинности. Это даёт возможность использовать действия, выбрав отдельные биты с помощью побитовых операций. Среди них наиболее известны следующие:
- конъюнкция — действие по смыслу приближённое к логическому умножению и союзу «и»;
- дизъюнкция — сложение напоминающее сравнение «или», то есть «или то, или это, или оба одновременно»;
- отрицание — операция над суждением с противоположным результатом начальному.
Последнее действие принято обозначать чертой, ставящейся над суждением. Кроме этого, могут использоваться операции исключающие «ИЛИ», эквивалентности, инверсии и сравнения. Но традиционным применением булевого типа считаются значения «да» / «нет».
Для реализации логических действий используются электрические схемы, называемые логическими элементами. В качестве данных используются сигналы с разным уровнем напряжения. На вход схемы подаётся значение, принимаемое за ноль или единицу, а с выхода снимается другое с определённым уровнем. То есть используется двоичная система счисления. Напряжение высокого значения принимается как истина, а низкого считается за ложь. Логические схемы позволяют в наглядном графическом виде отобразить последовательность операций при вычислении логических формул.
Такие логические элементы используют для организации работы компьютеров, схем автоматического контроля. Поэтому для любых видов сигналов характерны дискретные величины. При этом сам элемент может иметь как один, так и несколько входов, два или один выход. Традиционно элементы логики изготавливают в виде радиодеталей. Это интегральные микросхемы разного размера.
Таблица истинности
Любую логическую функцию можно описать с помощью таблицы истинности. То есть при выполнении действий их результатом будет два вида значение «истина» либо «ложь». Как оказалось, использовать таблицы для описания работы элементов довольно удобно. Причём вместо слов в ней ставят единицу либо ноль. Сложное логическое выражение обычно включает в себя несколько простых. Соединяет их операция.
Таблица истинности содержит все возможные комбинации переменных на входе и соответствующий результат их на выходе. Состоит она из 2n строк, где n — количество переменных, и n + m столбцов, у которых m — выходные данные. Если все строки известны, то исследуемый элемент, включающий функцию, называют частично определённый. Количество существующих операций зависит от числа высказываний. Если содержится 2n строк, то и всевозможных комбинаций будет 2n соответствующих значениям аргументов.
Строится таблица по простому принципу. В столбцах указываются номера входов и выходов, а строки заполняют соответствующими цифрами. Например, пусть имеется логический элемент с тремя выводами. Два из них входа X1 и X2, а один выход Y1. При подаче высокого напряжения сразу на два входных контакта на выходе устанавливается низкий уровень. В ином же случае всегда будет высокий. Для такой ситуации в первых двух столбцах проставляется все возможные варианты. Их будет четыре. В последней же колонке, советующей выходу, ставятся везде нули, кроме строчки, состоящей из двух единиц.
Построенная таблица является законченной основной характеристикой логического элемента. Работать с ней довольно удобно, так как наглядно и без дополнительных пояснений видно, какие сигналы установятся на выходе. Иногда есть смысл строить истинность для той или иной функции, используя лишь определённый набор заданных операций. Существует несколько возможностей описания:
- дизъюнктивная;
- конъюнктивная;
- алгебраическая нормальная.
Простой конъюнкцией называется система переменных, где каждая из них встречается только один раз. Если же объединить дизъюнкции с помощью конъюнкции, то можно получить совершённую конъюнктивную нормальную форму. В обратном случае возникнет дизъюнктивная составляющая.
Простейшие логические выражения
Любое утверждение строится из высказываний. Например, забор красный. Эта информация может быть правдивой или ложной. Утверждение может быть расширено так: забор красный или зелёный, цветной и деревянный. Смысл таких высказываний лежит в составных описывающих элементах. Наиболее часто используют три логические операции:
- «И» — оператор включает два высказывания, которые будут правдивыми, если они оба истинные. Если хотя бы одно из них ложь, то результат действия неверный.
- «ИЛИ» — составное утверждение правдивое тогда, когда любое из высказываний верное.
- «НЕ» — операция инверсии. Отрицание подразумевает противоположность над суждением. Если оно истинное, то итогом будет ложь, и наоборот.
В логических схемах используется для обозначения двоичный код состоящий из нуля и единицы. Так, для НЕ если на входе будет высокий уровень, то на выходе низкий. Наиболее наглядно получить представление о работе различных элементов можно, изучив их таблицу истинности. Для «И» она выглядит так:
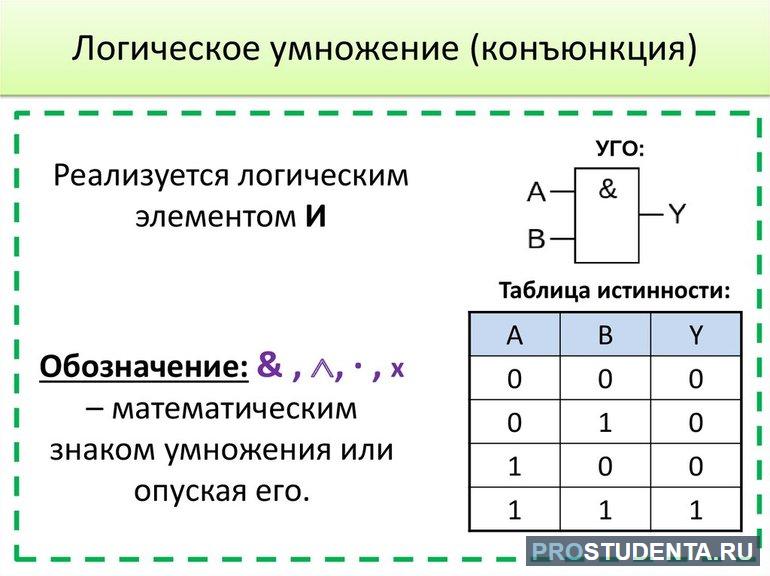
«И»
| А | Б | С |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| 1 | 1 | 1 |
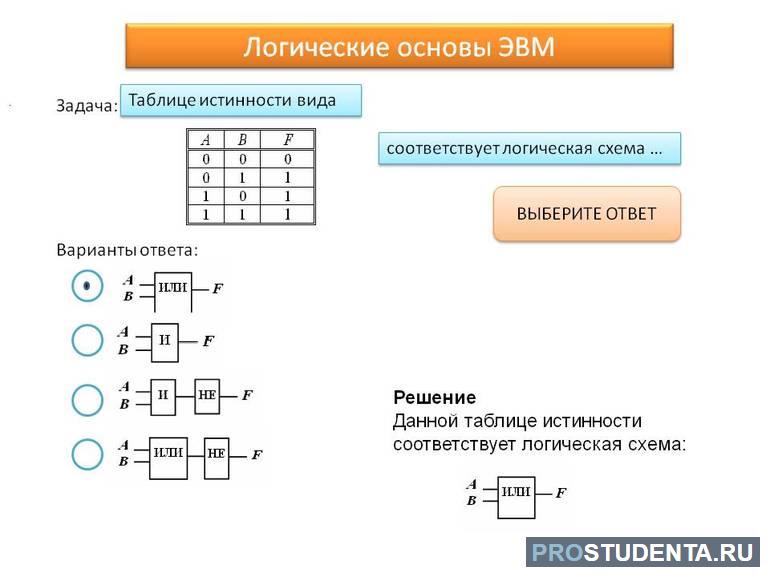
«ИЛИ»
| А | Б | С |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
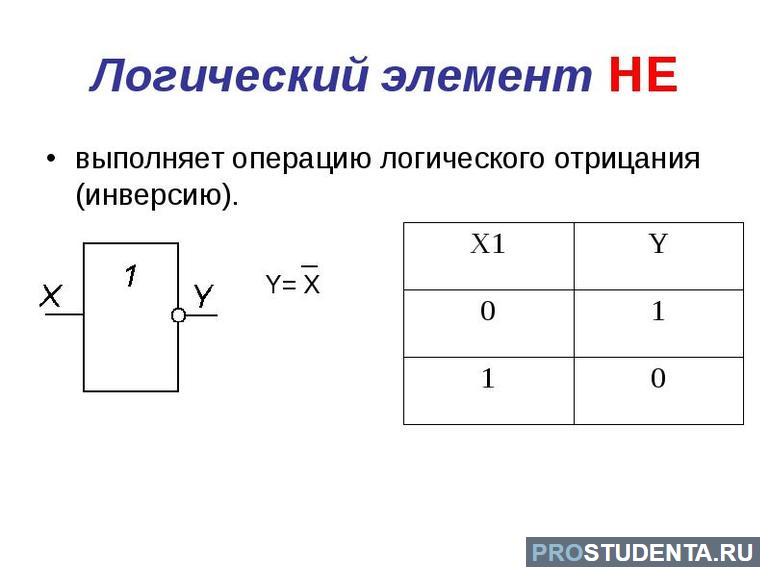
«НЕ»
| А | С |
| 0 | 1 |
| 1 | 0 |
В таблицах столбцы А и Б это входы логического элемента, а С — выход. Кроме простейших элементов, существуют и составные образованные различными комбинациями. Образовываются они с помощью объединения инверсного с другими типами. Так существует элемент «И-НЕ». В зарубежной литературе он будет обозначаться символом NAND. Он выполняет функцию «И» только выходной сигнал получается инвертированным. Там, где у простейшего элемента на выходе единица, у NAND будет ноль.
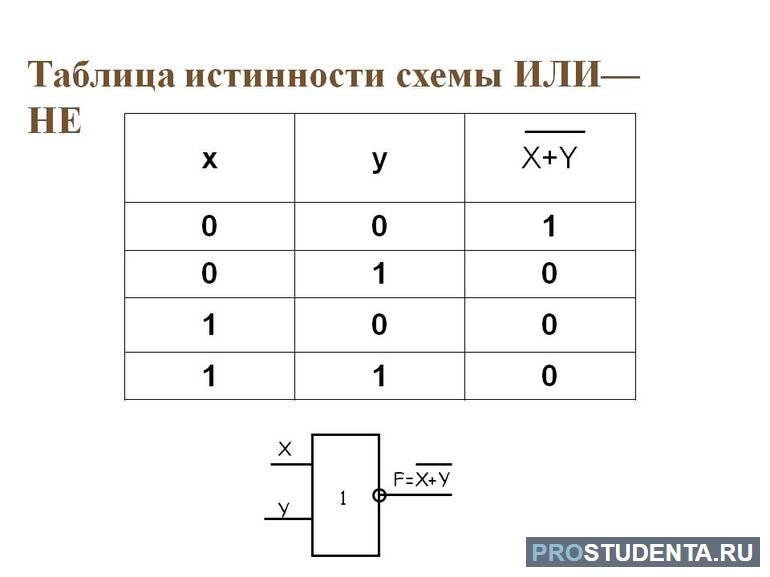
Вторым вариантом подключения будет объединение операторов «ИЛИ» и «НЕ». Обозначают его как NOR. Отличается он от простейшего только инвертированием результата. Ещё одним популярным элементом является «Исключающее ИЛИ» (XOR). Его называют сложение по модулю два. С помощью XOR организовывается работа сумматоров, популярных устройств в цифровой радиоэлектронике. У него на выходе будет единица в том случае, если на входы поступают разного уровня сигналы.
Рассмотренные элементы являются базовыми для построения интегральных микросхем. Как раз их работу и можно пояснить с помощью логических компонентов, вернее, их таблиц истинности. При этом элементы, выполняя определённую функцию (операцию) над входными сигналами (операндами, данными) обеспечивают нужный результат.
Решение задач
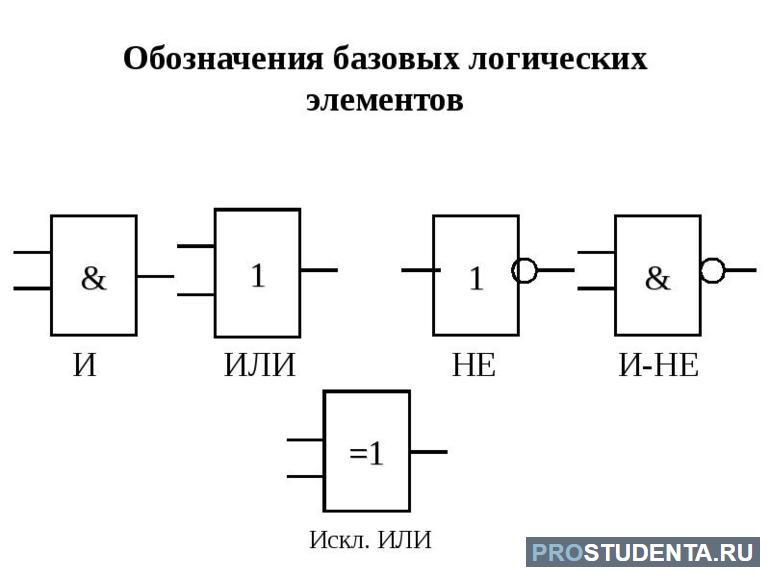
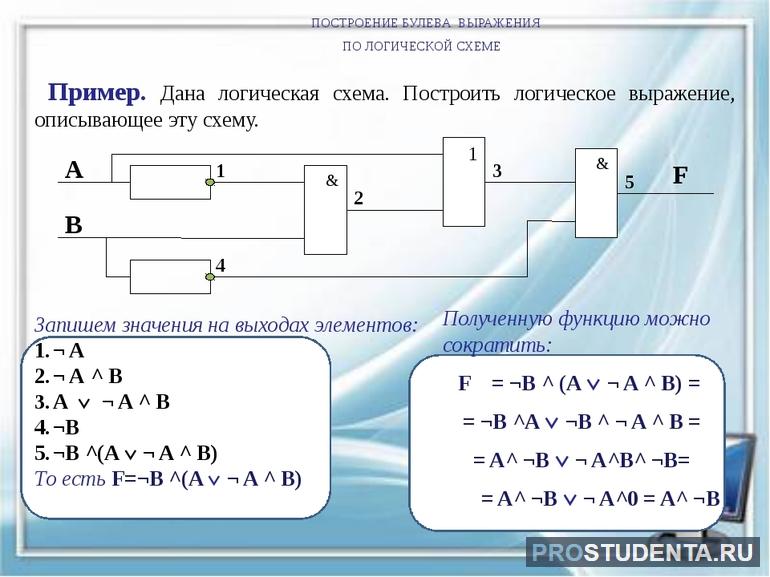
Логические элементы, применяемые в цифровой технике, имеют различные стандарты изображения. Чаще всего используется ANSI и IEC. Но на территории бывшего СССР применяют ГОСТ, согласно которому устройства обозначают треугольной или прямоугольной фигурой с выходящими из неё прямыми линиями. Те что справа принимаются за выходы, а слева — входы. В середине изображения ставится символ обозначающий тип элемента. Например, 1 — «НЕ», & - «И», ≥1 — «ИЛИ».
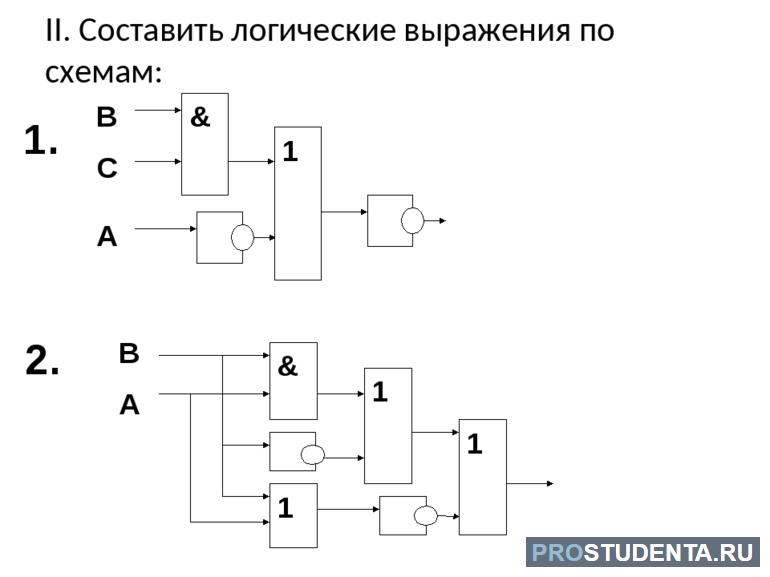
Реальные логические схемы могут содержать тысячи выводов. Их уравнения записывают по так называемой ярусной схеме, условно разделяя устройство на блоки. В общем случае решение задач выполняется по следующей последовательности действий:
- Определяется число входов и выходов элемента.
- Вычерчивается функциональная схема.
- Логическое устройство разбивается на ярусы, которым присваивают номера.
- Подписывают выводы элементов с обозначением названия искомой функции, снабжая её цифровым индексом. Обычно первая цифра — это номер яруса, а оставшиеся — порядковые номера в ярусе.
- Для каждого элемента составляют аналитическое выражение, определяющее его выходную функцию и переменные.
- Выполняют выражение одних выходных функций посредством других, пока не получится булева функция, определяемая входными переменными.
При решении задач используют законы булевой алгебры. Если формулы представляют одну и туже функцию, то их называют равносильными. Эта равнозначность доказывается алгебраическими правилами. Из основных теорем можно выделить: ассоциативность и коммутативность конъюнкции и дизъюнкции, дистрибутивность, идемпотентность. Правила соответствуют сочетательному, переместительному и распределительному законам.
Кроме этого, существуют специальные теоремы:
- двойное отрицание (y = y);
- свойство констант (y * 1 = y; y * 0 = 0; y v 0 = y; 0 = 1; 1 = 0);
- двойственности (y1 * y2 = y1 v y2);
- противоречия (y * y = 0);
- исключения третьего (y v y = 1).
Например, есть функция: f = s2 * s4 + s1 * s3 * s4 + s1 * s2 * s3. Её необходимо представить в виде базиса «И-НЕ». Решение будет выглядеть так: f = s2 s4 + s1 s3 s4 + s1 s2 s3 = s2 s4 + s1 s3 s4 + s1 s2 s3 = (s2 s4) * (s1 s3 s4) * (s1 s2 s3) = (s2|s4) * (s1|s3| s4) * (s1|s2|s3).
Следует отметить, что существуют и так называемые мажоритарные элементы. Это операнды, имеющие много входов. Например, переменная f на выходе четырёх ходового мажоритарного элемента примет 1, если как минимум три его входа будут соответствовать логической единице.



Ещё никто не комментировал эту статью. Оставьте комментарий первым!