Формулы поступательного и вращательного движения твёрдого тела

При изменении положения физической точки относительно выбранной системы говорят о выполнении механического перемещения. Существуют разнообразные способы его совершения. Одним из них является поступательное движение твёрдого тела. Вращательное перемещение интересно тем, что размерами объекта пренебречь нельзя. Значит, в описании процесса нужно использовать дополнительные величины, которые требуют понимания и изучения.

Оглавление:

• Общие сведения
• Период и частота
• Линейная и угловая скорость
• Ускорение движения

Общие сведения

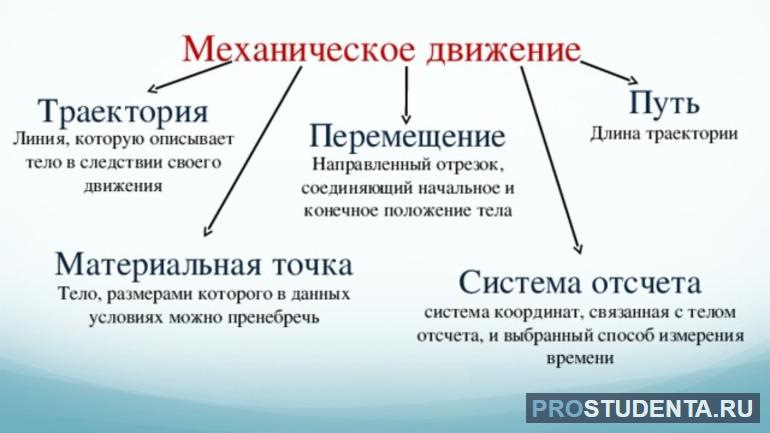
Механическим движением называют изменение положения тела относительно других объектов с течением времени. Например, езда на велосипеде, полёт мяча, бег спортсмена. При рассматривании таких процессов формы тел не учитываются. Это связано с тем, что их размеры по сравнению с пройденным расстоянием не имеют значения. Для таких случаев вводится понятие — материальная точка. То есть объекта, размерами которого можно пренебречь.

Описывают механическое движение с помощью трёх простейших величин:

• пути;
• скорости;
• времени перемещения.

Пусть имеется некое объёмное тело, например, книга. Если её взять и помахать ею в пространстве, то, можно сказать, что точки из которых она состоит движутся по-разному. Они имеют разную скорость, проходят различный путь. Следовательно, описать движение такого тела сложно. Именно поэтому вводят понятие материальной точки.

Но бывают такие ситуации, когда объект проходит путь, соизмеримый с размерами самого тела. В этом случае принимать его за точку нельзя. Можно представить, что предмет движется по дуге. Тогда скорости точек, из которых он состоит будут одинаковыми. Равным окажется и пройденный ими путь. Этот простейший вид движения называют поступательным. Другими словами, перемещением, при котором все его точки движутся одинаково.

Частным случаем такого изменения положения является вращательное движение. Из наиболее яркого примера можно привести вращение колеса. Рассматривая его, нужно отметить, что точки, расположенные ближе к центру, будут проходить меньшее расстояние, чем те, что находятся возле обода. Значит, и их скорости будут разными, поэтому в этом случае нужно учитывать размеры тела.

Так как для описания процесса использовать материальную точку нельзя, то и рассматривать движение с помощью скорости и расстояния будет неудобно и очень сложно. Вот почему изучают не траектории отдельных величин, а углы, на которые поворачиваются радиусы, количество оборотов. Следует отметить, что при вращательном движении все точки тела движутся по окружности, центры лежат на одной прямой. Называется она — осью.

Таким образом, под вращательным движением понимают такое изменение положение в пространстве, при котором все его точки перемещаются по окружностям с центрами, лежащими на одной прямой. При этом происходит этот процесс за время t.

Период и частота

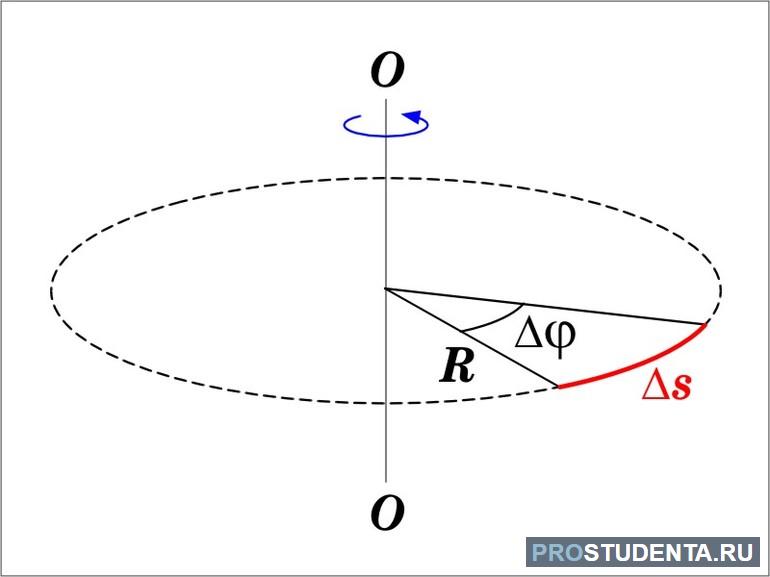
Пусть имеется тело цилиндрической формы. На нём можно выделить две точки: A и B. Они вращаются по окружности с разным радиусом. Первая расположена ближе к центру, значит, длина её траектории будет меньше, чем второй. Центры их движения лежат на одной прямой — оси вращения, проходящей через точку O.

За одно и то же время как A, так и B совершают поворот на один и тот же угол за равное время. Это утверждение справедливо, так как рассматривается вращение единого твёрдого тела. То есть такого предмета, расстояние между любыми точками которого всегда остаётся одинаковым. При движении цилиндра происходит одновременно поступательное и вращательное перемещение, поэтому сложное движение представляют как комбинацию этих двух видов изменений положения. Характеризуется оно двумя величинами:

• периодом;
• частотой.

Поворот на один оборот занимает определённое время. У него есть своё название — период вращения. Обозначается он буквой T. Измеряется в любых единицах времени. В СИ в их качестве приняты секунды [с]. Например, период вращения минутной стрелки составляет один час. Число оборотов, совершённых телом, обозначают буквой N.

Допустим, за 10 секунд тело совершит пять оборотов. Чтобы найти период, нужно время, за которое произошло одно вращение, поделить на совершённое их число. Значит, формула, связывающая обороты со временем и периодом, будет выглядеть так: T = t / N.

Можно представить, что тело совершает 10 оборотов за пять секунд. Для того чтобы найти, сколько понадобится времени для совершения одного вращения, нужно число всех оборотов разделить на время. Полученное значение называют частотой вращения (n). По сути, это величина, равняющаяся числу оборотов, совершаемых телом за единицу времени: n = N / t. Измеряется она в СИ в оборотах / секунду. Так как в числителе стоит безразмерная величина, то частоту измеряют в [c^-1]. Например, частота вращения Земли равняется одному обороту в сутки.

Между частотой и периодом существует связь. Если сравнить формулы, описывающие их, то можно заметить, что в них числитель и знаменатель поменялись местами. Значит, частота — это величина, обратная периоду: n = 1 / T. Соответственно, верным будет и равенство: T = 1 / n.

Линейная и угловая скорость

Любая точка, движущаяся вокруг оси, проходит определённый путь, который можно определить, зная её скорость и затраченное время. Пусть имеются две точки A и B, определяющиеся радиусами r1 и r2. При этом r2 больше r1. Скорость — это векторная величина. Она имеет направление. Поскольку за один оборот B проходит больше путь, то скорость её вращения будет превышать показатель для точки A, то есть V2 > V1. Параметр, определяющий скорость точек на вращающемся теле, называют линейным. Именно такими и являются V1 и V2.

Очевидно, что при вращательном движении линейные скорости постоянно изменяют своё направление. Но если рассматривать модуль величин, то для одних случаев перемещения он будет постоянным, а для других нет. Самый простой случай, который позволяет исследовать вращение является поступательный. Чтобы дать такому перемещению определение, нужно понимать, что равномерным в физике называют движение, при котором тело проходит равные участки пути за любые одинаковые промежутки времени.

Следовательно, равномерное вращение твёрдого предмета — это движение по окружности, при котором за любые равные промежутки времени тело поворачивается на одну и ту же величину угла. Другими словами, совершается одинаковое количество оборотов в выбранном временном интервале. Допустим, тело за секунду совершит один оборот. Если взять промежуток в десять раз больше, то отношение величин не изменится. То есть период и частота при равномерном вращении остаются постоянными.

Константой будет оставаться и линейная скорость. Но её значение зависит от расстояния, на котором находится точка от оси вращения. Когда A совершит один оборот, то пройденный ею путь будет равен длине окружности L. Чтобы найти скорость, нужно L разделить на время, затраченное на выполнение действия. Фактически им является период. Отсюда следует, что формулу для линейной скорости можно записать так: V = L / T. Так как длина окружности равняется 2pr, то выражение примет вид: V = 2pr / T. Но вращательное движение можно охарактеризовать и частотой. Поскольку T = 1 /n, формулу можно переписать: V = n * 2pr.

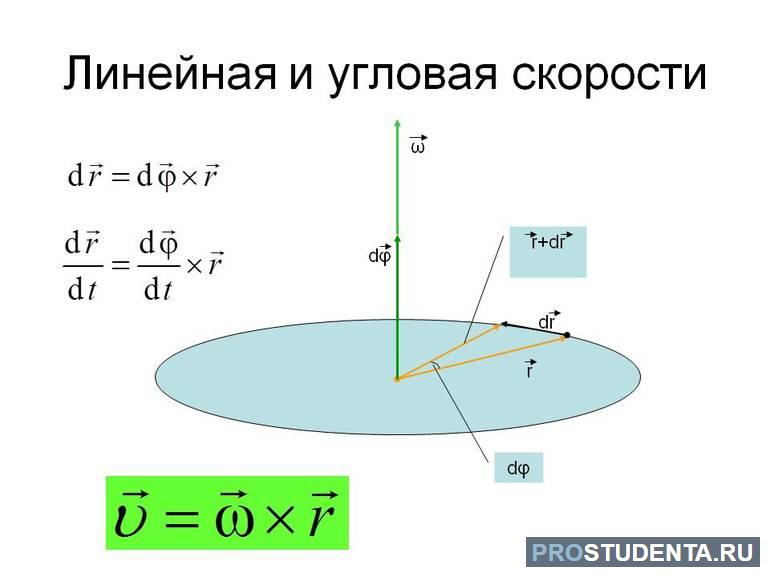
Охарактеризовать количественно вращение можно угловой скоростью. Это физическая величина, равная отношению угла поворота тела ко времени, за которое он произошёл.

Обозначается она ω и равняется ω = φ / t. Измеряется в радианах, делённых на секунду. При этом угол поворота радиуса φ одинаковый для любой точки в поворачивающимся твёрдом теле.

Ускорение движения

Если движение равномерное, то скорость тела направлена по касательной и связана с угловой соотношением V = ω * r. При этом точка испытывает ускорение, направленное к центру окружности. Вычисляется она по формуле: a = V² / r или a = ω ² * r. При повороте тела на небольшой угол φ угловую скорость можно определить из соотношения ω = Δ φ / Δ t, где:

• Δφ - угол поворота тела;
• Δt — время, за которое точка совершила поворот.

Если вращение абсолютно-равномерное, то Δt может быть любым. В ином случае ω является мгновенной угловой скоростью. При неравномерном движении V ≠ const, тогда ω тоже не будет постоянной величиной. Изменение Δω определяется разностью между принятым положением и начальным: Δω = ω - ω0.

Учитывая, что ускорение a = (V — V0) / Δt, по аналогии можно записать выражение: ω - ω0 / Δt. Это отношение называется угловым ускорением. Обозначают греческой буквой E. Находят же по формуле: E = Δ ω / Δ t. Измеряется ускорение в радианах, делённых на секунду в квадрате [рад/ с²]. Таким образом, угловым ускорением тела при вращательном движении называют физическую величину, равную отношению изменения угловой скорости за небольшой интервал времени к длительности этого промежутка.

Поскольку ускорение представляет собой изменение скорости ко времени, то можно записать: ΔV / Δt = ΔVr / Δt + Δ Ve / Δt, где: ΔVr — радиальное значение, ΔVe — угловое. Получается, что в выражении справа стоит ускорение a, а слева две составляющие, обусловленные криволинейностью и неравномерностью движения. Таким образом, полное ускорение представляет собой сумму двух взаимно перпендикулярных ускорений: a = ar + ae.

Следует отметить, что приведённые формулы справедливы не только для вращательного перемещения, но также и для возвратно-поступательного.

Если тело ускоряется, то угол между векторами ar и ae будет острым, при замедлении же он станет тупым. При этом вращение с постоянным угловым ускорение описывается выражением: ω(t) = ω0 + E * t.