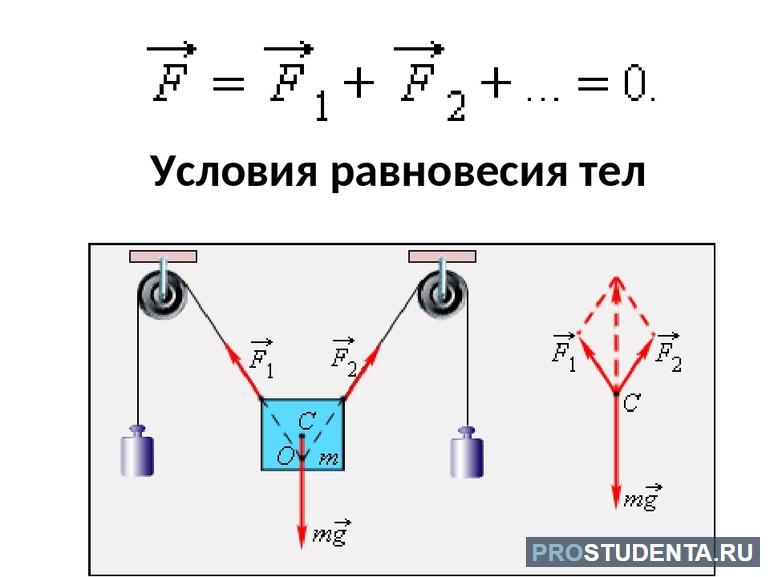
Условия равновесия тел в физике: формула и положения

Согласно второму закону Ньютона, условие равновесия тел выглядит следующим образом: если геометрическая сумма внешних сил, которые прилагаются к телу, равняется нулю, то оно находится в покое. Благодаря этому силы уравновешивают друг друга. На основе этого принципа действует множество предметов, включая весы.

Оглавление:

• Главное условие
• Крутящий момент и равновесие
• Нулевой показатель
• Двухкомпонентные силы

Главное условие

Первое условие равновесия заключается в том, что суммарная сила во всех направлениях должна быть нулевой.

Среди ключевых можно отметить следующие положения:

• Есть два условия, которые должны быть выполнены, чтобы объект находился в равновесии.
• Первое условие состоит в том, что чистая сила на объекте должна быть равна нулю, чтобы объект находился в необходимом состоянии.
• Если чистая сила равняется нулю, то она вдоль любого направления также будет приближена к этому показателю.

Основные термины, которые имеют отношение к уравновешиванию тел:

• сила — физическая величина, обозначающая способность толкать, тянуть, крутить или ускорять тело, которое измеряется в единицах, измеренных в массе x расстояние / время² (ML / T²);
• крутящий момент, предполагающий вращательное или скручивающее действие силы;
• передвижение — движение тела по линейной траектории, без деформации или вращения, то есть так, что каждая часть тела движется с одинаковой скоростью и в одном направлении; также (в физике) линейное движение тела рассматривается независимо от его вращения.

Чтобы объект находился в равновесии, он не должен испытывать ускорения. Это означает, что как чистое давление, так и чистый крутящий момент на объекте должны стремиться к значению «ноль».

В форме уравнения — это первое условие: F нетто=0

Для достижения этого условия действующие вдоль каждой оси движения должны суммироваться до нуля. Например, чистые внешние силы вдоль типичных осей x и y равны нулю. Это выглядит так: чистая Fx=0; чистая Fy = 0; F нетто = 0.

Если автомобиль находится в динамическом равновесии, то только потому, что он движется с постоянной скоростью. Существуют горизонтальные и вертикальные экспрессии, но чистая внешняя в любом направлении будет нулевой. Прилагаемое усилие между шинами и дорогой уравновешивается воздушным трением, а вес автомобиля поддерживается нормальным давлением, которые здесь показаны равными для всех четырех шин.

Крутящий момент и равновесие

Второе условие статического равновесия говорит о том, что чистый момент, действующий на объект, должен быть нулевым.

Это условие, необходимое для достижения равновесия, состоит в том, чтобы избежать ускоренного вращения. Вращающийся объект или система могут быть в равновесии, если их скорость постоянна и остается неизменной под давлением сил, действующих на него. Величина крутящего момента вокруг оси вращения определяется как τ=rFsinθ.

Крутящий момент в этом случае — вращательное действие силы, а равновесие представляет собой состояние тела в покое или в равномерном движении, результат всех сил которого равен нулю.

Детские качели являются отличным примером статического равновесия. Объект в статическом равновесии — это объект, который не имеет ускорения в любом направлении. Хотя может быть движение, которое будет постоянным.

Если этот объект находится в статическом равновесии, то момент на объекте должен равняться значению «ноль».

Нулевой показатель

Чистое давление, действующее на объект, должна быть равна нулю. Поэтому все силы уравновешиваются в каждом направлении. Например, автомобиль, движущийся по шоссе с постоянной скоростью, находится в равновесии, так как он не ускоряется ни в прямом, ни в вертикальном направлении. Математически это выражается как Fnet=ma=0.

Второе условие, необходимое для достижения равновесия, включает избегание ускоренного вращения (поддержание постоянной угловой скорости).

Вращающееся тело или система могут находиться в равновесии, если их скорость вращения постоянна и остается неизменной под действием процессов, влияющих на него.

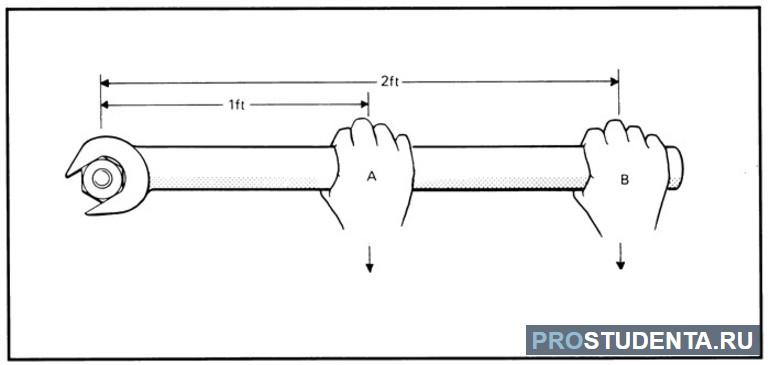
Чтобы понять, какие факторы влияют на вращение, необходимо обратить внимание на то, что происходит, когда открывается обычная дверь, вращающаяся на шарнирах. Величина, направление и точка приложения силы включены в определение физической величины, называемой крутящим моментом. Это вращательный эквивалент давления, а также мера эффективности силы в изменении или ускорении вращения (изменение угловой скорости за период времени).

В форме уравнения величина момента определяется как τ=rFsinθ, где τ (греческая буква тау) — символ крутящего момента, r — расстояние от точки поворота до точки, где применяется напряжение, F — величина, а θ - угол между силой и вектором, направленный от точки приложения к точке поворота.

Двухкомпонентные силы

В равновесии чистая сила и крутящий момент в любом конкретном направлении равны нулю.

Если суммарный момент инерции относительно оси равен нулю, объект не будет иметь ускорения вращения вокруг оси.

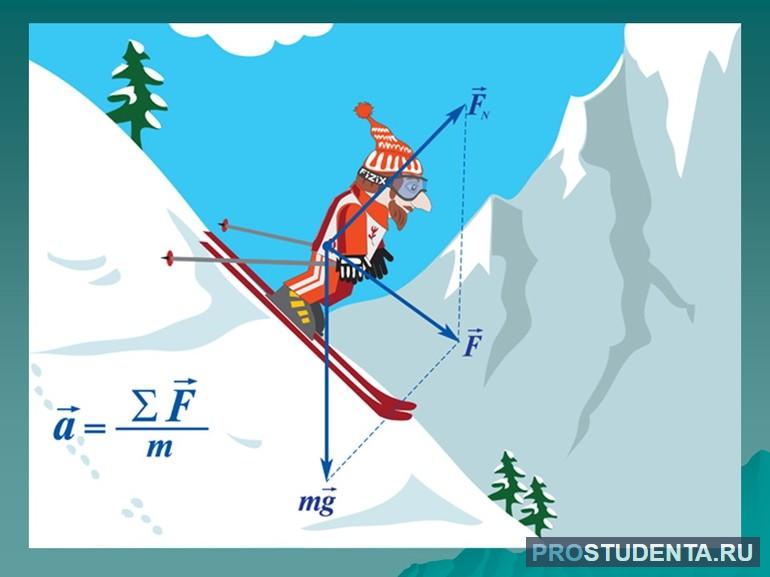
Объект с постоянной скоростью имеет нулевое ускорение. Неподвижный объект все еще имеет постоянную скорость, поэтому неподвижные объекты также отличаются отсутствием ускорения. Второй закон Ньютона гласит: ∑F=ma, поэтому объекты с постоянной скоростью также имеют нулевую чистую внешнюю силу. Это означает, что все силы, действующие на объект, сбалансированы, то есть находятся в равновесии.

Это правило также относится к механическому движению в определенном направлении. Если никакая чистая сила не приложена к объекту вдоль оси Х, он будет продолжать двигаться вдоль оси Х с постоянной скоростью, без ускорения. Это является основным учебным принципом статики.

Это правило можно легко распространить на ось Y. В любой системе, если приложенные силы не нейтрализуют друг друга, будет ускорение в направлении результирующей. В статических системах, в которых движение не происходит, сумма во всех направлениях всегда будет ноль. Эта концепция может быть представлена ​​математически с помощью следующих уравнений: ∑Fx=ma x=0.

Правило также относится к вращательному движению. Если результирующий момент относительно конкретной оси равен нулю, то тело находится в равновесии. Если он не вращается, то и не начнет вращаться. Если объект вращается, он будет продолжать вращаться с той же постоянной угловой скоростью. Опять же это можно распространить на моменты, связанные с осью Y.

Стоит отметить, что сила твердого материального вещества всегда будет отличаться от обычного варианта. Именно поэтому, чтобы четко сформулировать формулу, нужно учитывать вес и класс элемента.