Формулы математики 5 класса числовых и буквенных выражений

В средней школе применяются на уроке математики 5 класса формулы для числовых и буквенных выражений. Они используются для оптимизации вычислений и ускорения устного счета. Специалисты рекомендуют подробно изучить теоретические основы, поскольку материал является фундаментом для других дисциплин с физико-математическим уклоном. После его изучения необходимо переходить к решению задач.

Общие сведения

Некоторые новички очень часто не понимают основного отличия между числовым и алгебраическим выражениями. Школьную программу не все понимают. Однако проблема этого отличия является фундаментом всей математики, без которого не решаются задачи и не доказываются теоремы. Получить ответ на данный вопрос помогут определения, поскольку в них и содержится такая информация.

Числовое выражение — математическое тождество, состоящее только из цифр и знаков математических операций. Для чайников нужно привести следующие примеры:

1. 4+2-8-10: является числовым выражением.
2. 4++-4-555-6666-*+: набор математических символов.

Алгебраическим является числовое выражение, содержащее некоторые переменные (буквы).

Следует отметить, что его еще называют буквенным. Кроме того, любое из тождеств может включать в свой состав скобки круглой и квадратной форм.

Базовые арифметические операции

К базовым арифметическим операциям относятся основные действия над числами, а именно: сложение, вычитание, умножение и деление. Сложение обозначается символом "+" и состоит минимум из трех элементов. К ним принадлежат следующие: два слагаемых и результат, т. е. сумма.

Вычитание — операция, которая считается обратной сложению. Она состоит также минимум из трех компонентов: уменьшаемого (эквивалентного сумме), вычитаемого (первого слагаемого) и результата (II слагаемого). Обозначается символом "-".

Произведение — сложное арифметическое действие, состоящее также минимум из трех элементов. Обозначается символом "*". В некоторой литературе в буквенных выражениях можно увидеть, что символ произведения опускается, т. е. q*r=qr. Это сокращенная запись. Математики рекомендуют ее применять только в буквенных, поскольку она вызывает путаницу в числовых тождествах.

Следует отметить, что операция применяется, когда слагаемых очень много, т. е. они повторяются многократно. Например, тождество "3+3+3+3+3+3+3" можно записать в упрощенном варианте, т. е. 3*7. Числа "3" и "7" называются множителями или сомножителями, а их результат произведением.

Последней основной операцией является деление. Оно состоит из делимого, делителя и частного. Последний является результатом. Если провести аналогию с умножением, то делимое — произведение, делитель — I сомножитель, а частное — II множитель. Операция обозначается символами "/" и ":".

Следует отметить, что деление может содержать только два элемента (делимое и делитель). Это и есть основной отличительной особенностью от других операций. В этом случае частное записывается в виде обыкновенной дроби, т. е. 1/2. Последнее число можно оставить в таком виде или вычислить значение частного "0,5". Далее необходимо разобрать приоритетность каждой из операций.

Очередность действий

Приоритет любой операции задают специальные группировочные символы. Они называются скобками. Различают всего два вида, а именно: круглые — "()" и квадратные — "[]". Cледует отметить, что в математике применяются также и фигурный тип, но он не является группировочным символом для арифметических операций.

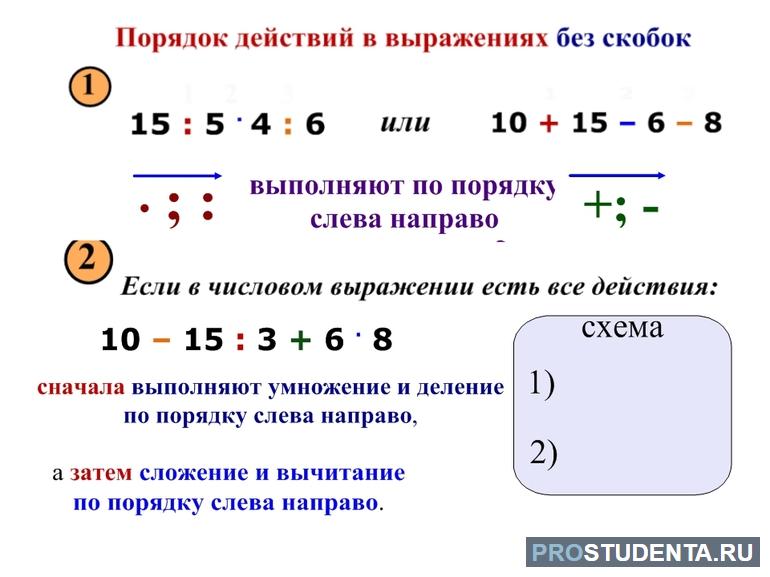
Когда в числовом или буквенном выражении отсутствуют группировочные элементы, тогда порядок операций устанавливается по-другому. Сначала выполняются умножение и деление, а затем — сложение и вычитание. Не имеет значения очередность выполнения деления или умножения, поскольку каждый сам выбирает последовательность для оптимизации вычислений.

Многие начинающие математики иногда забывают, что произведение обладает одинаковым приоритетом с делением, но сложение и вычитание — две операции, которые должны выполняться последними. Причем первоочередность у последних также не имеет значения, т. е. если удобно, то нужно выполнять сложение, а в противном случае — вычитание.

Далее нужно разобрать, как решать буквенные выражения, а также тождества числового типа. Для этой цели имеются в дисциплине "математика для 5 класса" правила и формулы.

Оптимизация расчетов

Умение правильно решать числовые и буквенные выражения в 5 классе является базовым. Они позволяют упростить любое тождество, доказать теорему и просто выполнить быстро вычисления в уме.

Например, необходимо определить значение выражения "4997*5". В этом случае многие постараются воспользоваться калькулятором. Однако эта мера — лишняя. Для этого достаточно просто выполнить определенные математические преобразования, т. е. 4997*5=(5000-3)*5=25000-15=24985.

Для буквенных выражений также существуют определенные соотношения. Они называются формулами сокращенного умножения, и позволяют понижать степень элементов. Соотношения имеют следующий вид:

1. m^3-n^3=(m-n)(m^2+mn+n^2) и m^3+n^3=(m+n)(m^2-mn+n^2).
2. (m+n)^3=m^3+3mn^2+3nm^2+n^3 и (m-n)^3=m^3-3mn^2+3nm^2-n^3.
3. m^2-n^2=(m-n)(m+n).
4. (m+n)^2=m^2+2mn+n^2 и (m-n)^2=m^2-2mn+n^2.

Выражения буквенного типа, находящиеся в первой группе, называются разностью и суммой кубов двух величин соответственно. Их рекомендуется использовать для понижения третьей степени многочлена. Они также очень часто используются для операций упрощения и решения уравнений.

Вторая группа формул позволяет "свернуть" многочлен третьей степени в более компактную форму. Соотношения называются кубом суммы или разности двух элементов. Тождество обладает очень сложной структурой, а эту особенность требуется учитывать при ведении расчетов.

Третья группа похожа на первую, но она включает всего одно соотношение. Последнее применяется только для упрощения и решения выражений с неизвестными величинами. Четвертая группа, как и вторая, выполняет аналогичные функции.

Следует отметить, что математики рекомендуют выполнять составление числовых и буквенных тождеств для тренировок самостоятельно. Они могут быть представлены в виде выражений, обыкновенных дробей или уравнений.

Таким образом, числовые и алгебраические выражения занимают главное место в математике и являются базовыми компонентами любой дисциплины с физико-математическим уклоном.

В средней школе применяются на уроке математики 5 класса формулы для числовых и буквенных выражений. Они используются для оптимизации вычислений и ускорения устного счета. Специалисты рекомендуют подробно изучить теоретические основы, поскольку материал является фундаментом для других дисциплин с физико-математическим уклоном. После его изучения необходимо переходить к решению задач.

Общие сведения

Некоторые новички очень часто не понимают основного отличия между числовым и алгебраическим выражениями. Школьную программу не все понимают. Однако проблема этого отличия является фундаментом всей математики, без которого не решаются задачи и не доказываются теоремы. Получить ответ на данный вопрос помогут определения, поскольку в них и содержится такая информация.

Числовое выражение — математическое тождество, состоящее только из цифр и знаков математических операций. Для чайников нужно привести следующие примеры:

1. 4+2-8-10: является числовым выражением.
2. 4++-4-555-6666-*+: набор математических символов.

Алгебраическим является числовое выражение, содержащее некоторые переменные (буквы).

Следует отметить, что его еще называют буквенным. Кроме того, любое из тождеств может включать в свой состав скобки круглой и квадратной форм.

Базовые арифметические операции

К базовым арифметическим операциям относятся основные действия над числами, а именно: сложение, вычитание, умножение и деление. Сложение обозначается символом "+" и состоит минимум из трех элементов. К ним принадлежат следующие: два слагаемых и результат, т. е. сумма.

Вычитание — операция, которая считается обратной сложению. Она состоит также минимум из трех компонентов: уменьшаемого (эквивалентного сумме), вычитаемого (первого слагаемого) и результата (II слагаемого). Обозначается символом "-".

Произведение — сложное арифметическое действие, состоящее также минимум из трех элементов. Обозначается символом "*". В некоторой литературе в буквенных выражениях можно увидеть, что символ произведения опускается, т. е. q*r=qr. Это сокращенная запись. Математики рекомендуют ее применять только в буквенных, поскольку она вызывает путаницу в числовых тождествах.

Следует отметить, что операция применяется, когда слагаемых очень много, т. е. они повторяются многократно. Например, тождество "3+3+3+3+3+3+3" можно записать в упрощенном варианте, т. е. 3*7. Числа "3" и "7" называются множителями или сомножителями, а их результат произведением.

Последней основной операцией является деление. Оно состоит из делимого, делителя и частного. Последний является результатом. Если провести аналогию с умножением, то делимое — произведение, делитель — I сомножитель, а частное — II множитель. Операция обозначается символами "/" и ":".

Следует отметить, что деление может содержать только два элемента (делимое и делитель). Это и есть основной отличительной особенностью от других операций. В этом случае частное записывается в виде обыкновенной дроби, т. е. 1/2. Последнее число можно оставить в таком виде или вычислить значение частного "0,5". Далее необходимо разобрать приоритетность каждой из операций.

Очередность действий

Приоритет любой операции задают специальные группировочные символы. Они называются скобками. Различают всего два вида, а именно: круглые — "()" и квадратные — "[]". Cледует отметить, что в математике применяются также и фигурный тип, но он не является группировочным символом для арифметических операций.

Когда в числовом или буквенном выражении отсутствуют группировочные элементы, тогда порядок операций устанавливается по-другому. Сначала выполняются умножение и деление, а затем — сложение и вычитание. Не имеет значения очередность выполнения деления или умножения, поскольку каждый сам выбирает последовательность для оптимизации вычислений.

Многие начинающие математики иногда забывают, что произведение обладает одинаковым приоритетом с делением, но сложение и вычитание — две операции, которые должны выполняться последними. Причем первоочередность у последних также не имеет значения, т. е. если удобно, то нужно выполнять сложение, а в противном случае — вычитание.

Далее нужно разобрать, как решать буквенные выражения, а также тождества числового типа. Для этой цели имеются в дисциплине "математика для 5 класса" правила и формулы.

Оптимизация расчетов

Умение правильно решать числовые и буквенные выражения в 5 классе является базовым. Они позволяют упростить любое тождество, доказать теорему и просто выполнить быстро вычисления в уме.

Например, необходимо определить значение выражения "4997*5". В этом случае многие постараются воспользоваться калькулятором. Однако эта мера — лишняя. Для этого достаточно просто выполнить определенные математические преобразования, т. е. 4997*5=(5000-3)*5=25000-15=24985.

Для буквенных выражений также существуют определенные соотношения. Они называются формулами сокращенного умножения, и позволяют понижать степень элементов. Соотношения имеют следующий вид:

1. m^3-n^3=(m-n)(m^2+mn+n^2) и m^3+n^3=(m+n)(m^2-mn+n^2).
2. (m+n)^3=m^3+3mn^2+3nm^2+n^3 и (m-n)^3=m^3-3mn^2+3nm^2-n^3.
3. m^2-n^2=(m-n)(m+n).
4. (m+n)^2=m^2+2mn+n^2 и (m-n)^2=m^2-2mn+n^2.

Выражения буквенного типа, находящиеся в первой группе, называются разностью и суммой кубов двух величин соответственно. Их рекомендуется использовать для понижения третьей степени многочлена. Они также очень часто используются для операций упрощения и решения уравнений.

Вторая группа формул позволяет "свернуть" многочлен третьей степени в более компактную форму. Соотношения называются кубом суммы или разности двух элементов. Тождество обладает очень сложной структурой, а эту особенность требуется учитывать при ведении расчетов.

Третья группа похожа на первую, но она включает всего одно соотношение. Последнее применяется только для упрощения и решения выражений с неизвестными величинами. Четвертая группа, как и вторая, выполняет аналогичные функции.

Следует отметить, что математики рекомендуют выполнять составление числовых и буквенных тождеств для тренировок самостоятельно. Они могут быть представлены в виде выражений, обыкновенных дробей или уравнений.

Таким образом, числовые и алгебраические выражения занимают главное место в математике и являются базовыми компонентами любой дисциплины с физико-математическим уклоном.