Понятие дроби в математике 5 класса и основные ее свойства

Не всегда числа выражаются целыми величинами. Понятие дроби в математике 5 класса рассматривается более подробно, поскольку каждый ученик должен понимать основные принципы работы с числами любого формата. Это позволит грамотно выполнять вычисления, используя свойства дробных выражений. Специалисты рекомендуют изучить теорию, а затем перейти к ее практическому применению.

Оглавление:

• Применение дробных величин
• Классификация дробей
• Смешанная форма

Общие сведения

Числа делятся на целые и дробные. К первым относится множество всех натуральных величин, используемых при устном счете. Однако не все значения можно записать, воспользовавшись первым типом. Например, может быть не целый торт, а его половина. Для этой цели были придуманы дроби, характеризующие некоторую часть от целого. Чтобы понять основную разницу между величинами, нужно разобрать объяснение дробей для 5 класса и примеры их применения.

Дробь — значение, которое применяется для точного представления числовой формы. Для иллюстрации определения на практике нужно рассмотреть такой пример: при расчетах ускорения свободного падения была получена величина «9,81».

Если использовать приближенное целое значение, получаются числа 9 и 10. Однако при решении задачи по физике необходимо брать точное выражение. При отказе от подробного представления появится большая погрешность при вычислениях. Далее необходимо разобрать дробные величины подробно, чтобы любой ребенок мог производить без особого труда действия над ними.

Применение дробных величин

Для сравнения необходимо решить задачу по физике и рассчитать силу тяжести «Fт» физического тела, масса которого составляет 100 кг. Формула для расчета имеет такой вид: Fт=m*g, где m — масса тела и g — ускорение свободного падения. Далее следует разобрать два случая:

1. Приближенный.
2. Точный.

Для приближенного расчета соотношение будет выглядеть следующим образом: Fт = 9 * 100 = 900 (Н) и Fт = 10 * 100 = 1000 (Н). При точном вычислении: Fт = 9,81 * 100 = 981 (Н). Следует отметить, что в первом случае наблюдаются значительные погрешности, как в большую, так и в меньшую сторону, т. е. 981−900=81 и 1000−981=19. Этого допускать нельзя.

Для иллюстрации необходимости использования дробных величин была подобрана задача по физике, поскольку нужно было доказать ученикам, насколько она связана с математикой. Далее необходимо разобрать классификацию дробей.

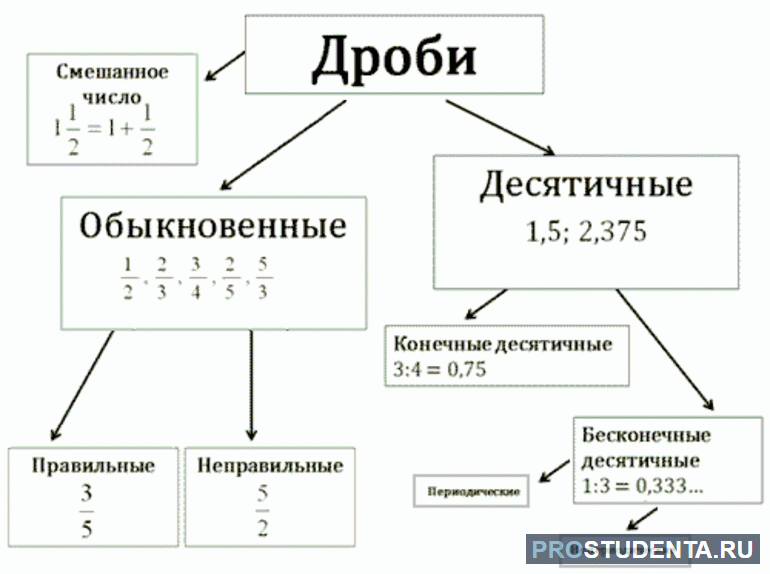
Классификация дробей

Дробные величины математики делят на 3 вида. К ним относятся:

1. Десятичные.
2. Обыкновенные.
3. Смешанные формы.

В первом случае любое дробное значение, состоящее из дробной части, отделенной от целого выражения точкой или запятой, называется десятичной дробью. Последняя бывает в двух формах, а именно: конечной и бесконечной. Первая характеризуется ограниченным количеством знаков после запятой (точки). Например, величина 0,2356 состоит из целой части (0) и дробной (2356).

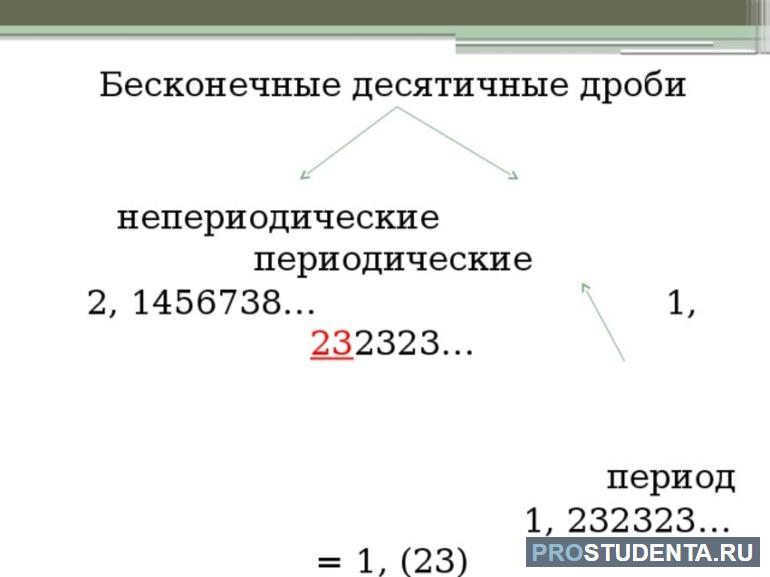
Бесконечная дробь классифицируется на 2 типа. К ним относятся следующие:

1. Периодическая.
2. Непериодическая.

К первой относятся все бесконечные десятичные дробные выражения, знаки которых после запятой повторяются по определенному закону. Повторяющиеся символы необходимо брать в круглые скобки (указывать период). При этом запись выглядит более компактной, т. е. 0,(13). Однако не во всех случаях величину можно записать на листке бумаги. Эту операцию невозможно осуществить для бесконечной непериодической. Очень часто ее округляют до определенной величины, а именно: до десятых, сотых долей и т. д.

Кроме десятичных, бывают еще и обыкновенные дробные величины. Они состоят из верхней и нижней частей, разделенными между собой косой чертой «/". Примером является число, записанное в общем виде «W/V», где W — числитель и V — знаменатель. В зависимости от последних параметров, обыкновенные дроби классифицируются на 2 вида:

1. Правильные.
2. Неправильные.

У первых числитель меньше, чем знаменатель. В этом случае справедливо условие W<V. Если последнее неравенство не выполняется, можно сделать вывод о принадлежности дробного значения ко второму виду. Существует еще одна форма представления дробных элементов, но ее необходимо разобрать отдельно.

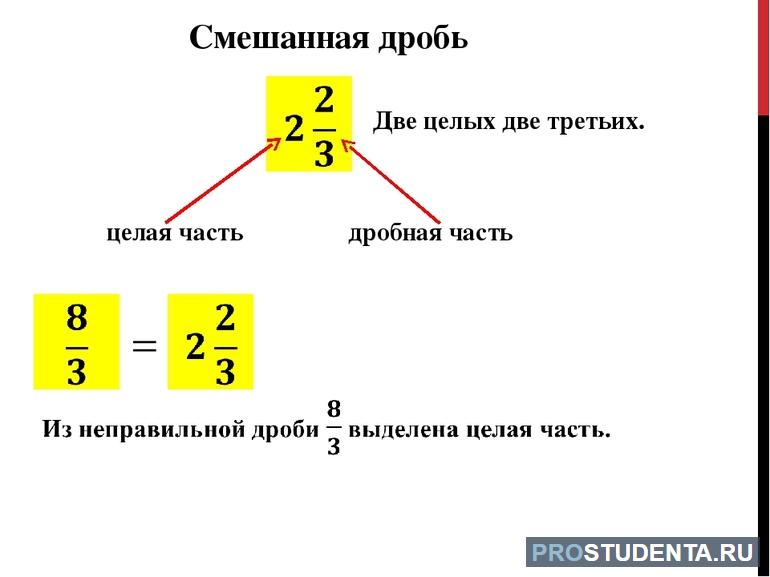
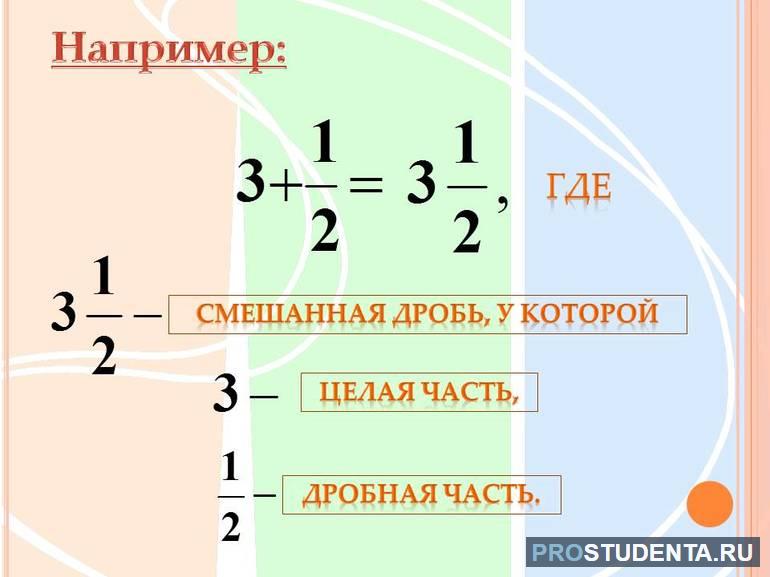
Смешанная форма

Смешанным числом называется величина, включающая целую и дробную части. Такие формы образуются при помощи десятичных и обыкновенных дробей. Суть преобразований для каждого случая является различной.

Для смешанного выражения, образованного десятичной дробью, нужно разобрать пример самого числа «5,526». Оно состоит из целого (5) и дробного элемента (526). Его получают при делении одной величины на другую. В конкретном примере делимое равно 5526, а делитель — 1000, т. е. первая величина примерно в 5 раз больше второй. Для преобразования существует очень простой алгоритм, который легко объяснить, воспользовавшись следующими пунктами:

1. Записать величину: 0,12.
2. Обозначить числитель (соответствует дробной части после запятой): 12.
3. Определить знаменатель (эквивалентен десяти в степени, равной количеству знаков в дробной части): 10 ² .
4. Написать результат: 12/100.

Величина, полученная в пункте 4, может быть преобразована при помощи сокращения: 12/100=(4*3)/(4*25)=3/25. Ученикам требуется обратить внимание, как решать пример. Для начала нужно вынести общий множитель для числителя и знаменателя, разложив их на сомножители: 12=4*3 и 100=4*25. После этого нужно сократить на 4.

Смешанное число, состоящее из целого компонента и правильной дроби, образуется из неправильного дробного тождества. Операция позволяет выделить целый элемент. Алгоритм преобразования:

1. Записывается искомая неправильная дробь: W/V.
2. Выделяется целый компонент, при делении числителя на знаменатель (берется только целое число без учета дробной составляющей): R=W/V.
3. Рассчитывается величина нового числителя: W'=W-RV.
4. Записывается искомый результат: R[W'/V].

Если нужно выполнить обратную операцию по конвертации смешанного элемента в неправильную дробь, можно воспользоваться специальной методикой:

1. Написать число в смешанной обыкновенной форме: R[W'/V].
2. Вычислить значение нового числителя W по следующему соотношению: W=VR+W'.
3. Записать искомый результат: W/V.

Методики расписаны во многих учебниках и позволяют решить дроби в 5 классе без ошибок. Специалисты рекомендуют выписать их на отдельный лист бумаги и положить «перед глазами». Однако со временем надобность в шпаргалке отпадет, поскольку действия при регулярных занятиях будут отточены до автоматизма. Далее необходимо затронуть тему об основных свойствах дробей.

Важные свойства

Каждая из дробей обладает определенными свойствами. Для десятичной они являются следующими:

1. Десятичная дробная величина — частное, полученное в результате операции деления двух чисел.
2. У дробной части можно дописать любое количество нулей, т. е. 0,5=0,500000000000. При этом величина конечной и начальной дробей не изменится.
3. Любую десятичную дробную величину можно представить в виде обыкновенной.

Далее необходимо рассмотреть основные свойства обыкновенных дробей:

1. При умножении числителя и знаменателя на одно и то же числовое значение величина дроби не изменится, т. е. 9/10=(8*9)/(8*10).
2. Если к числителю прибавить одно значение, а затем его отнять, величина дробного выражения не изменится, т. е. (9+3−3)/10=9/10. Для знаменателя можно также воспользоваться аналогичным свойством: 9/(10+3−3).
3. Произведение обратных обыкновенных дробей эквивалентно единице, т. е. (5/8) * (8/5) = 1.
4. Если поделить одну обыкновенную дробную величину на обратную, получится исходное число в квадрате, т. е. (5/8): (8/5) = 25/64.

Следует отметить, что свойства необходимо применять при решении различных задач, доказательства теорем и выведения различных соотношений, поэтому нужно научиться производить различные действия над дробями.

Таким образом, дроби применяются в математике для вычислений точных значений, которые используются при расчетах различных величин, характеризующих процессы, явления и количественные характеристики.