Способ перевести десятичную дробь в обыкновенную: правила

При изучении математики важно не только знать, как перевести десятичную дробь в обыкновенную, но и уметь применять полученные знания на практике. Обучают этой науке в четвертом классе средней школы. Преобразование выражений позволяет упрощать различные задачи, делая решение простым и понятным. Сама операция несложная, но требует понимания смысла использования дробных чисел. Лишь в этом случае действие можно будет довести до автоматизма и выполнять устно.

Оглавление:

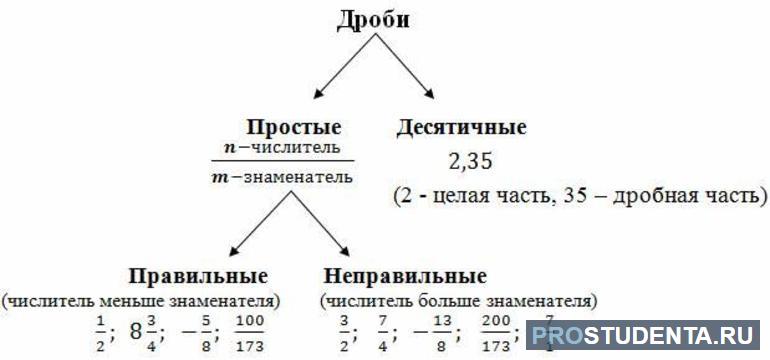
• Виды дробей
• Алгоритм преобразования
• Решение примеров
• Использование онлайн-конвертера

Виды дробей

Дробь — это число, в состав которого входит одна доля или несколько её частей, поделенных на равные части. По сути, это отношение двух значений. Обыкновенное дробное выражение записывают с помощью натуральных чисел, разделённых горизонтальной чертой. Называется она винкулумом. В литературе можно встретить и другой тип записи с наклонной чертой (солидус).

Верхнее число, или стоящее слева от черты, называют числителем или делимым, а нижнее — знаменателем (делителем). Что такое дробь, удобнее всего объяснить на примере. Пусть на столе стоит тарелка, на которой лежит пирог. Он один и целый. Можно взять нож и разделить его на шесть равных частей.

По сути, количество пирога не изменится, поэтому, с математической точки зрения, на тарелке будет всё так же находиться целый пирог. Если с неё взять два куска, то целостность нарушится. Записывают это действие с помощью дроби: 2/6. То есть внизу указывают число, обозначающее, на сколько поделили пирог, а сверху — сколько кусков забрали.

Дробь — это число, обозначающее часть целого предмета. При этом дробное отношение всегда будет меньше единицы. Существующие отношения принято разделять на следующие виды:

1. Правильные — отношения, в которых числитель меньше знаменателя.
2. Неправильные — дроби, где делимое по величине превышает делитель.
3. Смешанные — состоящие из суммы натурального и дробного числа.
4. Десятичные — в знаменателе которых стоит натуральное число с размерностью кратной десяти.
5. Составные — состоящие из нескольких черт дроби.

С дробными отношениями можно выполнять любые математические действия. Их складывают, вычитают, умножают, возводят в степень. Замечательным свойством дробей есть возможность их преобразования из одного вида в другой. Например, можно перевести обычную дробь в десятичную, неправильную — в смешанную. При этом операции возможны как в одну, так и другую сторону.

Существует и так называемое основное свойство отношений. Оно позволяет над числителем и знаменателем проводить одинаковые операции

. Например, делитель и делимое можно возвести в одинаковую степень, поделить или умножить на одно и то же число. Это свойство позволяет упрощать выражения, делая их простыми и удобными для восприятия.

Алгоритм преобразования

Действие по переводу десятичной дроби в простую относится к элементарным операциям. Существует несколько способов перевода. Какой из них выполнять, зависит от личных предпочтений решающего. Например, выражение 3,2 можно записать и как 16/5.

Другими словами, математики договорились, что в случае простых чисел нули опускаются, а вместо них ставится запятая, отделяющая целую часть. Это было сделано для удобства восприятия записи и облегчения счёта.

Правило наиболее часто используемого способа перевода следующее. Если в знаменателе стоит число, кратное десяти, то нужно просто переписать числитель, а затем отсчитать число цифр, совпадающих с разрядностью числа в знаменателе, и поставить после них запятую. Счёт числа отделяемых цифр нужно начинать с правой стороны. При этом если количество нулей превышает число цифр в делителе, то недостающее их количество записать перед числом.

При преобразовании смешанного числа в десятичное действие немного изменяется. Вначале нужно записать целую часть отношения. После него поставить запятую, а уже затем написать число из делимого дробной части с учётом недостающих нулей.

Проводимые операции, кроме получения периодической дроби, можно выполнять и в обратную сторону. Остаток при делении должен всегда быть меньше делителя. Поэтому, если при действии получается ноль, деление прекращается, а если остаток — бесконечная периодическое отношение.

Чаще всего для того, чтобы преобразовать простую дробь в десятичную, необходимо выполнить три шага:

1. Сократить выражение, требующее преобразования.
2. Разделить удобным способом числитель на знаменатель. В зависимости от величины значений, стоящих в числителе и знаменателе, это можно сделать столбиком или в уме. Если при делении остаток выходит отличным от нуля, то поставить запятую и продолжить искать частное.
3. Записать найденный результат с использованием запятой.

Нужно отметить, что алгоритм, объясняющий правило того, как перевести обыкновенную дробь в десятичную, подходит лишь для случаев, когда знаменатель раскладывается на множители пять и два. В иных случая получится периодическое десятичное число.

Решение примеров

Порой теоретическая информация довольно трудно воспринимается без применения её на практике. Поэтому крайне важно не только посмотреть, как делает преобразование учитель, но и самостоятельно выполнить перевод. Обычно хватает трех-четырех примеров для каждого типа преобразований, чтобы закрепить материал и освоить практическое применение.

Существуют определённые сборники заданий, предназначенные для самостоятельного решения учащимися. Вот некоторые наиболее интересные примеры из них:

1. Преобразовать: 1/1000; 34/10; 78954/10; 186/100; 959/10000. Алгоритм действия определяется правилом отсчитывания запятой. В задании три нуля, но в числителе только один знак. Поэтому на недостающих местах следует поставить нули. Отсюда следует что 1/1000 = 0,001. По аналогии нужно решать и следующие примеры. В итоге должно получиться: 34/10 = 3,4; 78954/10 = 7895,4; 186/100 = 1,86; 959/10000 = 0,0959.
2. Записать выражения в обыкновенном виде: 0,59; 34,78; 0,00078; 767,009. В соответствии с правилом в числителе записывают исходное число, а в знаменатель ставят единицу: 0,59 = 0,59/1. Для избавления от запятой делимое и делитель умножают на сто, так как по условию после запятой стоит два знака: (0,59 * 100) / (1 * 100) = 59/100. Аналогично решают и оставшиеся примеры: 34,78 = 34,78/1 = 34,78 * 100/ 100 = 3478/100; 0,00078 = 78/100000 = 39/50000; 767,009 = 767 + 0,009= 767 9/1000.
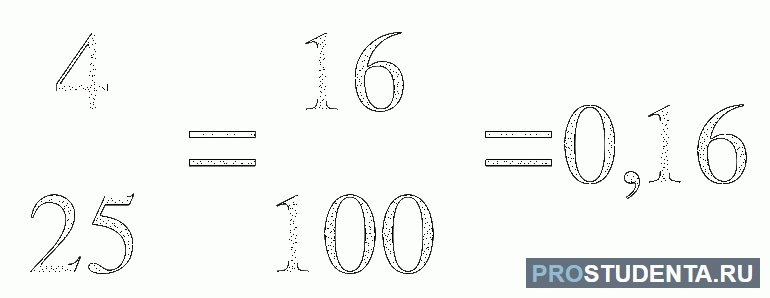
3. Перевести выражения в десятичный вид: 5/2; ¼; 34/81; 456/1245; 1245/456. Преобразование таких примеров можно выполнить путём деления числителя на знаменатель для нахождения частного. В первом случае пять нужно разделить на два. Используя деление в столбик, можно опередить, что целым будет число два (2 * 2 = 4). Так как в остатке получается единица, то в частном ставят запятую, а к остатку дописывают ноль. То есть, 5/2 = 2,5. Таким же образом переводят и другие примеры: ¼ = 0,25; 34/81 = 0,420; 456/1245 = 0,366; 1245/456 = 2,73.

Эти задания затрагивают преобразование как в одну, так и в другую сторону. После первичного перевода не стоит забывать об упрощении полученного результата. Его нужно делать всегда, чтобы в дальнейшем при решении сложных задач последующие действия становились проще.

Использование онлайн-конвертера

Десятичные дроби могут состоять из довольно больших чисел. Поэтому не всегда их можно быстро преобразовать. При этом любая невнимательность может привести к ошибке, что повлечёт неверный как промежуточный, так и итоговый результат. В таких случаях есть резон использовать так называемый конвертер дробей.

Это интернет-сервис, предоставляющий услуги по автоматическому преобразованию дробей из одного вида в другой. Для того чтобы воспользоваться его возможностями, пользователю даже необязательно понимать принцип перевода выражений. От него требуется лишь ввести исходные данные в предлагаемую форму и нажать кнопку «Рассчитать».

Таких математических сервисов в интернете довольно много. Русскоязычные конвертеры не требуют регистрации и указания каких-либо персональных данных. При этом свои услуги они предоставляют бесплатно. Согласно отзывам пользователей, можно выделить следующие онлайн-калькуляторы:

• 0oq;
• onlinemschool;
• naobumium;
• allcalc;
• webmath.

Нужно отметить, что приведенные сайты являются настоящими математическими комбайнами-решателями. Они умеют не только конвертировать дроби, но и выполнять с ними любые действия. Например, складывать, делить, умножать, извлекать корень и возводить в степень. Кроме этого, на их страницах содержится теоретический материал и подробное описание решений.