Определение, свойства и признаки прямоугольника

В геометрии встречается класс задач, связанные со свойствами прямоугольника. Определение этой геометрической фигуры — четырехугольник с прямыми углами, противоположные стороны которого равны между собой и параллельны друг другу. Прямой угол — это угол, градусная мера которого составляет 90 градусов. Особое свойство этой фигуры описано в теореме Пифагора — квадрат его диагонали равен сумме квадратов двух его смежных сторон. Частный случай прямоугольника — квадрат.

Оглавление:

• Признаки прямоугольника
• Свойства параллелограмма
• Формулы для определения параметров
• Пример решения задачи

Признаки прямоугольника

Определение прямоугольника, или параллелограмма, происходит на основании теоремы плоскостной геометрии или, как ее еще называют, евклидовой. Она имеет такую формулировку: при равенстве трех углов градусной мере в 90 градусов и эквивалентности только противолежащих сторон фигура является прямоугольником. Доказать теорему можно следующим образом:

1. Обозначить фигуру четырьмя литерами из английского алфавита: UVWZ.
2. Углы при вершинах: ∠U=∠V=∠W=90.
3. На основании утверждение о сумме углов четырехугольника необходимо найти ∠Z: ∠Z=360-(90+90+90)=90.
4. Фигура обладает попарно противолежащими, параллельными и равными между собой сторонами. Соответственно, она образует прямые углы, так как при таком типе сторон, какими обладает параллелограмм, углы могут быть только 90 градусов.
5. Если сравнить полученные данные с определением прямоугольника, то можно сделать вывод о том, что искомая фигура им и является.

Четвертый шаг можно проверить на практике. Для этого нужно начертить фигуру с параллельными противоположными сторонами разной длины, т. е. UV||WZ, UV=3 см и WZ=5 см. После этого точки V и W нужно соединить отрезком между собой. Аналогичную операцию нужно выполнить и для точек U и Z.

Кроме того, существуют доказательства других теорем. Математики вывели следующие признаки принадлежности четырехугольника к классу прямоугольников:

1. Равенство, перпендикулярность и параллельность только противоположных сторон.
2. Диагонали равны и образуют при пересечении пару тупых и острых вертикальных углов.
3. Формулировка теоремы из евклидовой геометрии о трех прямых углах.

Следует отметить, что для точной идентификации прямоугольника трех признаков будет достаточно. После этой операции необходимо перейти к изучению свойств фигуры.

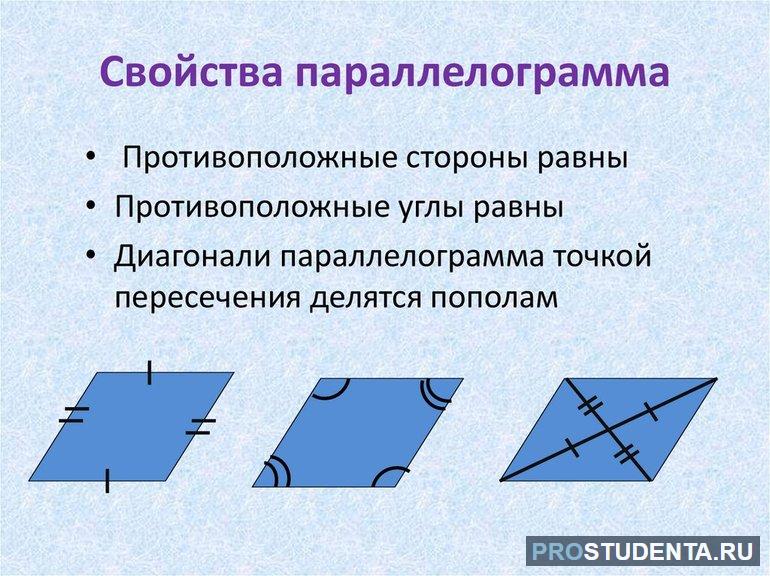
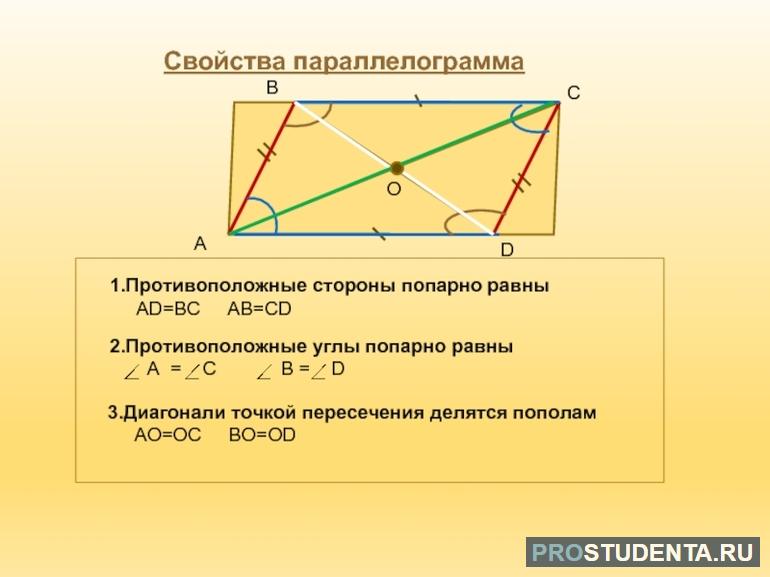
Свойства параллелограмма

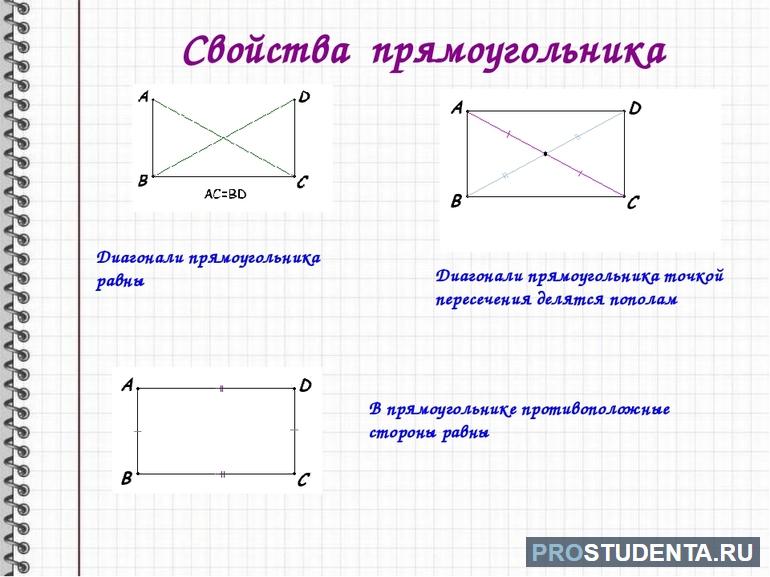
При решении задач по геометрии или доказательстве некоторых утверждений рекомендуется применять уже готовые варианты. Они бывают следующими:

1. Равны и перпендикулярны между собой противолежащие стороны.
2. Внутренние углы равны, а их сумма равна 360 градусам.
3. Величины диагоналей равны между собой.
4. Произведение диагоналей равно сумме квадратов смежных сторон фигуры, исходящих из одной вершины.
5. Стороны противоположные друг другу не являются равными между собой.
6. Диагонали делятся точкой их пересечения на четыре одинаковых отрезка.
7. Точка, образованная пересечением диагоналей, является центром фигуры и вписанной окружности.

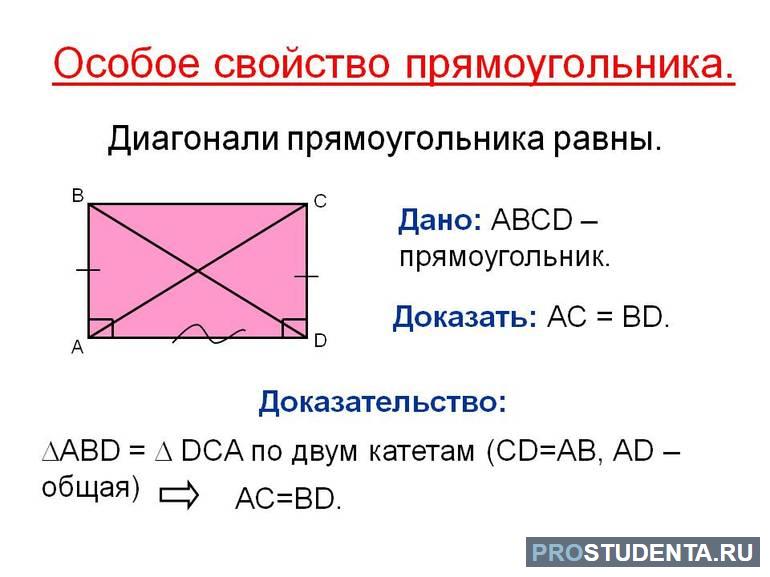
Следует отметить, что равенство двух диагоналей доказывается при помощи простых математических операций. Для этого нужно выполнить следующие действия:

1. Начертить прямоугольник UVWZ и провести в нем диагонали VZ и UW. Они пересекутся в некоторой точке S.
2. Необходимо рассмотреть оба прямоугольных треугольника UVZ и UWZ. Они равны между собой, по следующему признаку: катеты — противоположные равные стороны (угол между ними равен 90).
3. На основании второго пункта можно сделать вывод о равенстве треугольников. Следовательно, также равны и их гипотенузы. Последние являются диагоналями.

Для доказательства четвертого свойства рекомендуется воспользоваться теоремой Пифагора. В этом случае нужно рассматривать прямоугольные треугольники (UVZ и UWZ), у которых гипотенузы — диагонали (VZ и UW). Для этого нужно выразить каждую из последних через катеты: VZ^2=UV^2+VW^2 и UW^2=UZ^2+WZ^2.

Если учитывать, что по третьему свойству диагонали равны, то можно формулу записать в особом виде, поскольку достаточно взять любые смежные стороны фигуры. Соотношение выглядит следующим образом: VZ*UW=UV^2+VW^2. Однако последнего недостаточно при нахождении параметров прямоугольника. Для этой цели необходимо использовать следствия из теорем в виде математических записей.

Формулы для определения параметров

Для удобства необходимо ввести обозначение различных параметров прямоугольника. К ним относятся следующие:

1. Стороны: большая - m, меньшая - n.
2. Диагональ: o.
3. Периметр: Р.
4. Площадь: S.
5. Углы при пересечении диагоналей: острый - ∠t, тупой - ∠T.
6. Радиус вписанного круга: R.

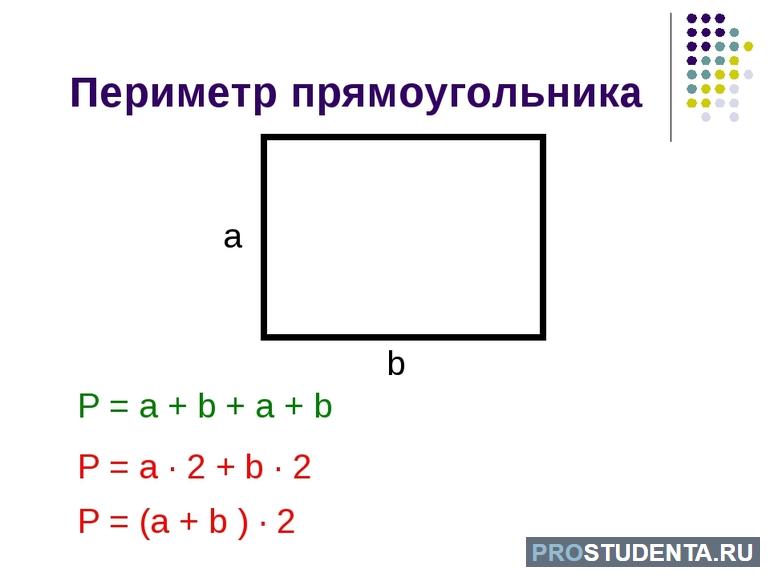
Периметром называется параметр прямоугольника, определяющий суммарное значение длины всех сторон фигуры. Площадь — размерность в двумерном пространстве. Далее нужно ознакомиться с основными соотношениями, связывающими основные параметры фигуры. К ним относятся следующие:

1. Определение периметра: Р=2(m+n)=2[m+S/m]=2[n+S/n]=2[m+(4R^2-m^2)^(1/2)]=2[n+(4R^2-n^2)^(1/2)].
2. Нахождение размерности: S=mn=m[(H-2m)/2]=n[(H-2n)/2]={[Pm]-2m^2}/2={[Pn]-2n^2}/2=o^2 * sin(t) * 0,5=m[4R^2-m^2]^(1/2)=n[4R^2-n^2]^(1/2).
3. Pадиус вписанной окружности: R=[m^2+n^2]^(1/2)/2=(P² - 4Рm+8m²)^(1/2)/4=(P² - 4Pn+8n²)^(1/2)/4=0,5(S² +n⁴)^(1/2)/n.

Cледует отметить, что величину радиуса вписанного круга можно еще вычислить при известном значении угла между стороной и диагональю по формуле: R=m/[2sin(T')], где Т' — величина угла между m и о. Существует и другое соотношение через косинус, но оно имеет более сложный вид, т. е. R=0,25(m+n-o)/[cos(T')]. Последнее выражение очень часто не используется в геометрии, но о нем необходимо знать.

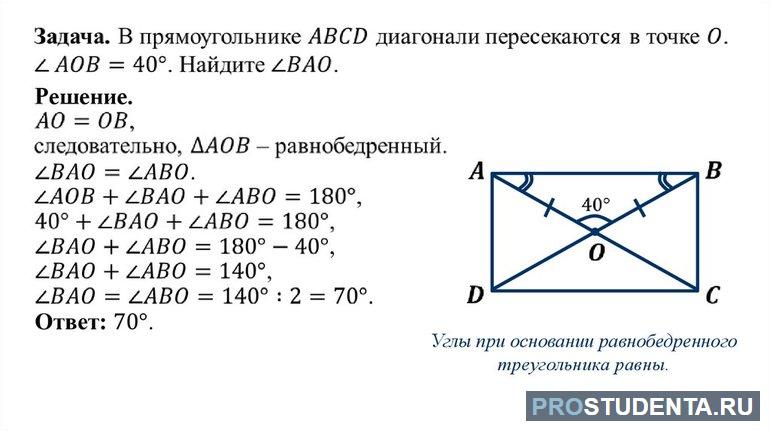
Пример решения задачи

На плоскости изображен четырехугольник с тремя прямыми углами. Его стороны неизвестны, но одна из них больше другой на 2 см. Диагонали геометрического тела равны и образуют две пары вертикальных углов (тупых и острых), а также эквивалентны среднему арифметическому большей и удвоенному значению меньшей стороны. Необходимо определить следующие параметры фигуры:

1. Стороны.
2. Диагональ.
3. Периметр.
4. Площадь.
5. Углы между диагоналями.
6. Среднюю линию.

Для решения задачи необходимо применить определенный алгоритм, при помощи которого выполняется пошаговое вычисление параметров фигуры. Он имеет следующий вид:

1. Определение типа фигуры: прямоугольник, т. к. диагонали равны, образуют 2 пары вертикальных углов и три угла между сторонами эквивалентны 90 градусам.
2. Обозначить вершины фигуры: UVWZ.
3. Провести диагональ UW.
4. Малая (n) сторона эквивалентна неизвестной s, а большая (m) — s+2.
5. Диагональ о: о=(s+2+2s)/2=(3s+2)/2.
6. Составить уравнение нахождения диагонали, используя формулу o^2=m^2+n^2: [(3s+2)/2]^2=s^2+(s+2)^2.
7. Раскрыть скобки в выражении, полученном на шестом шаге: 2,25s^2+3s+1=2s^2+4s+4.
8. Перенести переменные влево, а константы — вправо: 2,25s^2-2s^2+3s-4s=1-4.
9. Привести подобные элементы: 0,25s^2-s-3=0.
10. Вычислить дискриминант: D=1+4*3*0,25=2^2.
11. Найти корни по формулам: s1=(1-2)/0,5=-2 (не подходит, поскольку длина стороны всегда больше 0) и s2=(1+2)/0,5=6 (см).
12. Вычисление большей стороны: m=6+2=8 (см).
13. Расчет диагонали: о=(8+6*2)/2=10 (см).
14. Вычисление периметра: Р=2(m+n)=28 (cм).
15. Значение площади: S=6*8=48 (см^2).
16. Найти меньший ∠t между диагоналями из формулы S=o^2 *sin(t): sin(t)=S/o^2=48/100=0,48 (). ∠t=arcsin(0,48)=28,6854 (градусов).
17. Вычисление величины большего угла Т: ∠Т=180-∠t=151,3146 (градусов).
18. Величины средней линии (отрезка, соединяющего средние точки меньших сторон) эквивалентна длине m.

Таким образом, при решении задач рекомендуется сначала идентифицировать прямоугольник при помощи признаков, а затем воспользоваться его свойствами и соотношениями для нахождения неизвестных параметров.