Правила по сложению и вычитанию дробей (математика, 5 класс)
После рассмотрения натуральных чисел и действий над ними переходят к изучению правил сложения и вычитания дробей. На математике в 5 классе этой теме уделяется несколько уроков. Преподаватель не только даёт алгоритм вычислений, но и учит школьников применять знания на практике. Научиться правильно и быстро выполнять эти алгебраические действия важно, так как в дальнейшем это умение приходиться использовать практически при изучении любой науки.
Оглавление:
Общие сведения
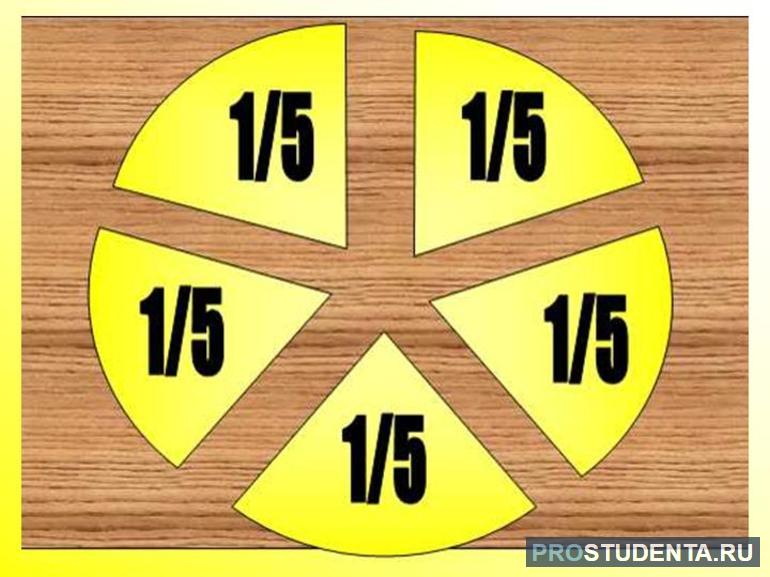
Дробные числа получаются в том случае, если один предмет необходимо разделить на несколько одинаковых частей. Проще всего разобраться в понятии можно на простом примере. Пусть имеется пирог круглой формы. Если разрезать его на четыре равные части, то говорят о четвертине, а если на две — половине. Но в математике эти слова имеют свои названия. Четвертину называют одна четвёртая, половину — одна вторая. Записывают их как отношение и используют для этого дробную черту.
По сути, дробное выражение представляет собой операцию деления. Например, если имеющийся торт нужно разделит на три равные части, то это действие можно записать как 1: 3. Полученные куски называют долями, а в математике — дроби. То есть каждая часть в примере, будет составлять от целого одну третью. Записывают это так: 1 / 3. Число, стоящее под чертой, показывает то, что торт был разделён на три равные части, а над ней — обозначает количество взятых долей.
Так как справедливо записать равенство 1:3 = 1 / 3, то к числам можно применить терминологию, использующуюся при делении. Верхнее называют делимым, а нижнее — делителем. Но для понимания, что речь идёт о дроби, в таких выражения используют свои названия — числитель и знаменатель. Черту же называют дробной. Поэтому можно сказать, что знаменатель показывает, на сколько равных частей разделили целое число, а числитель — сколько одинаковых долей было взято.
Например, был испечён один торт. За ужином съели от него 4 / 6. Руководствоваться нужно тем, что в знаменателе стоит число, которое показывает, как было разделено целое, а в числителе, сколько забрано. Поэтому можно утверждать, что торт был разделён на шесть кусков, из которых четыре были съедены. Так как одна доля равняется 1 / 6, то на столе останется 2 / 6.
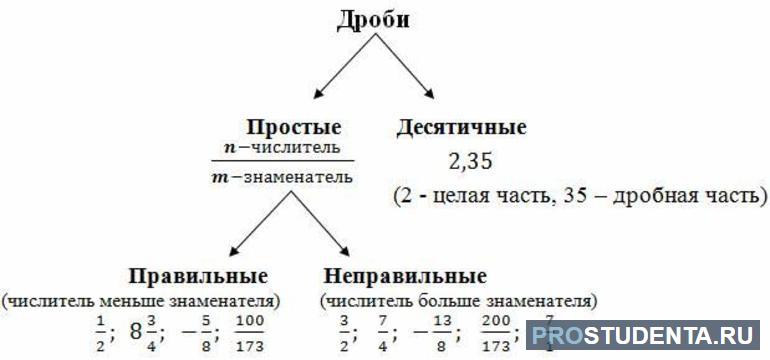
Существующие дроби разделяют по видам. Они бывают:
- правильные — выражения у которых значение числителя меньше знаменателя;
- неправильные — делимое больше или равно делителю;
- смешанные — комбинированное дробное выражение, состоящее из целого числа и неправильной дроби.
Так как дробные выражения, по сути, числа, то над ними можно выполнять любые арифметические операции, например, складывать, отнимать. Но при этом перед тем как решать задания на сложение и вычитание обыкновенных дробей, в 5 классе учат их вначале преобразовывать и упрощать.
Свойства дробей
Пусть дана некоторая дробь вида a / b. Оказывается, что, если числитель и знаменатель умножить на одно и то же число, например, с, результат действия не изменится: a / b = (a * c) / (b * c). Этот закон получил название — основное свойство дроби. Он особенно актуален при выполнении операций сложения и вычитания, так как позволяет привести выражение к простому виду.
Доказать правило можно следующим образом. Пусть есть отношение a / b равное к. Из него можно выразить числитель, используя определение частного: a = b * k. Это выражение можно умножить на некое число неравное нулю. В результате получится равенство: a * c = (b * k) * c. В правой части записано произведение. Поэтому можно воспользоваться переместительным законом и переписать уравнение как a * c = (b * c) * k. Из полученного выражения k = (a * c) / (b * c). Отсюда следует, что a / b = (a * c) / (b * c). Свойство доказано.
Второе свойство можно сформулировать так: если есть дробь a / b, то при изменении знака перед числителем и всей дроби результат не изменится. То есть, a / b = - (- a / b). Это утверждение справедливо и для действия по отношению к знаменателю. Доказывается это правило следующим образом. Пусть есть равенство: (-a / b) = k. Числитель можно выразить из определения частного: -a = b * k. Это соотношение можно домножить на -1. Тогда равенство примет вид: a = - b * k. Если выразить k, то получится -k = a / b → k = - (a / b), что и следовало доказать.
При решении определённых примеров есть смысл приводить дроби к одному виду. Для этого существуют следующие правила:
- Чтобы привести смешанную дробь в неправильную нужно целую часть умножить на знаменатель, а потом прибавить к полученному результату числитель. Затем, делитель оставить без изменения, а в числитель записать сумму. Например, 3 (½) = ((3 * 2) + 1) / 2 = 7 / 2.
- Для преобразования неправильного выражения в смешанное нужно выделить из дроби целую часть, а остаток занести в числитель, оставив знаменатель без изменения. Для нахождения целого можно воспользоваться правилом деления в столбик. Например, 18 / 5 = 3 (3/5).
Стоит отметить, особенность смешанной дроби. Её запись вида c (a / b) подразумевает, что между целой частью и отношением стоит знак плюс. То есть, по сути, c (a / b) = с + (a / b).
Усвоив рассмотренные правила, можно переходить к непосредственному изучению математических алгоритмов складывания и вычитания дробей.
Правила действий
Чтобы научиться быстро прибавлять и вычитать дроби, нужно понимать правило приведения к общему знаменателю. Когда имеются выражения, над которыми необходимо выполнить действия, при этом у них разные делили, нужно выполнить преобразование. Например, пусть имеется дробь 3 / 5. Надо сделать так, чтобы в делителе стояло число 40. Согласно основному свойству числитель и знаменатель можно умножить на одно и то же число. Поэтому можно записать так: 3 / 5 = (3 * 8) / 40 = 24 / 40. Другими словами, числитель увеличивается на множитель, равный числу, на которое поменялся знаменатель.
Таким образом, если имеются две дроби с разными делителями, то чтобы найти для них общее число, следует подобрать наименьшее значение, которое делится на один и другой знаменатель без остатка. Фактически это получается наименьшее общее кратное. Найти его можно, выполняя следующую последовательность действий:
- разложить каждый знаменатель на множители;
- из полученного ряда убрать повторяющиеся цифры;
- найти произведение оставшихся чисел, которое и будет искомым общим знаменателем.
Итак, существует два случая, с которыми можно столкнуться при прибавлении или вычитании. Первый достаточно простой, но при этом является частным случаем второго. Для лучшего восприятия алгоритм для каждого из случаев удобно записать в виде таблицы.
| Вид операции | Правило выполнения | Формула |
| Одинаковые знаменатели |
|
|
| Разные знаменатели |
|
|
Нужно отметить, что операции со смешанными дробями ничем не отличаются от рассмотренных выше. Единственно, действия с целыми частями выполняются отдельно от дробных, а затем записывается совместный результат.
Примеры решений
Подробное решение примеров дробей для 5 класса с объяснением поможет лучше разобраться в теоретическом материале. При этом полученный опыт позволит самостоятельно решать задания любой сложности. Вот типичные задачи, которые используются в рамках подготовки учеников в средних образовательных школах:
- Найти результат действия: 3 / 14 + 10 / 21. Дроби в выражении имеют разные знаменатели. Согласно алгоритму, их нужно привести к общему знаменателю, а затем с его помощью найти дополнительные множители. Для этого 14 и 42 следует разложить на простые числа: 14 = 2 * 7; 42 = 2 * 3 * 7. Отсюда следует, что НОЗ = 2 * 7 * 3 = 42. Далее, всё по алгоритму: ((3* 3) / 42) + ((2 * 10) / 42) = (9 / 42) + (20 / 42) = (9 + 20) / 42 = 29 / 42.
- Определить разность: 26 / 40 — 9 / 25. Пример решается аналогично предыдущему, но перед поиском НОЗ, первый член можно упростить. Для этого числитель и знаменатель нужно разделить на два: 26 / 40 = 13 / 20. Придерживаясь последовательности действий решение можно записать так: 13 / 20 — 9 / 25 = ((13 * 5) / 100) — ((9 * 4) / 100) = (65 — 36) / 100 = 29 / 100.
- Вычислить ответ: 3 (5/8) — 1 (9/10). В этом случае удобно целые части вычесть отдельно от дробных. Тогда, решение будет выполнено за два действия. Первое 3 — 1 = 2. Второе (5 / 8) — (9 / 10) = ((5 * 5) / 40) — ((4 * 9) / 40) = (25 — 36) / 40 = - 11 / 40. Таким образом, ответ будет: 2 (-11/40). Такая запись некорректная, поэтому из целого нужно вычесть дробное выражение. В итоге получится: (2 / 1) — (11 / 40) = (80 — 11) / 40 = 69 / 40 = 1 (29 / 40).
- Найти результат действия: 1 (2/5) + 4 / 5. В этом случае смешанное число удобно перевести в неправильную дробь, а уже после, выполнить сложение. Так, 1 (2/5) = ((1 * 5) + 2) / 6 = 7 / 5. Теперь получились две дроби с одинаковым знаменателем. Воспользовавшись алгоритмом из таблицы, найти их сумму будет несложно: 7 / 5 + 4 / 5 = (7 + 4) / 5 = 11 /5 = 2 (1/5).
Следует отметить, что последний пример можно решить, и не преобразуя смешанную дробь в неправильную. Можно выражение расписать как 1 (2/5) + 4 / 5= 1/ 1 + 2 / 5 + 4 / 5, а затем рассчитать ответ за два действия. Какой способ использовать, принципиальной разницы нет, но, пожалуй, первый удобнее и быстрее.







Ещё никто не комментировал эту статью. Оставьте комментарий первым!