Формула и определение закона сохранения энергии

Пожалуй, самым важным явлением природы открытым человечеством стал закон сохранения энергии. Его определение и формула нашли широкое применение в развитии техники. Например, при изучении трения, проектирования электромоторов. Осознание того, что значение энергии в замкнутой системе — величина постоянная, позволило отказаться от утопических идей по изобретению вечных двигателей и направить усилия на усовершенствования методов увеличения полезной работы.

Оглавление:

• Общие сведения
• Полная энергия
• Закон сохранения
• Решение задач

Общие сведения

Для того чтобы выполнить какое-либо действие, например, поднять вес, передвинуть предмет, ударить по поверхности, нужно выполнить работу. В физике под ней понимают скалярную величину, являющуюся мерой силы, приложенной к телу или системе. Зависит она от численного значения направления и перемещения. Если вещество или физическая совокупность способна совершить работу, то говорят, что оно обладает энергией. Другими словами, физической величиной, характеризующей способность тела выполнять действие.

Обозначают энергию буквой E. Измеряется она в тех же единицах, что и работа — джоулях [Дж]. Наглядно показать выполнение действия с затратой энергии можно на примере с механическими часами. Так, для того чтобы они показывали правильное время, их необходимо завести. Делается это с помощью колесика, при вращении которого сжимается пружина. Ей передаётся энергия, и она способна совершать работу по приведению в действие часового механизма. По мере того как пружина распрямляется, её сила уменьшается. Следовательно, выполнение работы сопровождается изменением энергии.

Впервые термин «энергия» использовал Аристотель. Под ним он понимал жизнедеятельность человека. В 1686 году Лейбниц расширил формулировку, охарактеризовав слово «живой силой», которую определил как произведение массы тела на скорость. В 1807 году Томас Юнг смог открыть связь энергии с работой. Много лет велись споры, что же она собой представляет — субстанцию или физическую величину. В итоге учёные пришли к мнению, что энергия — это мера движения и взаимодействия тел.

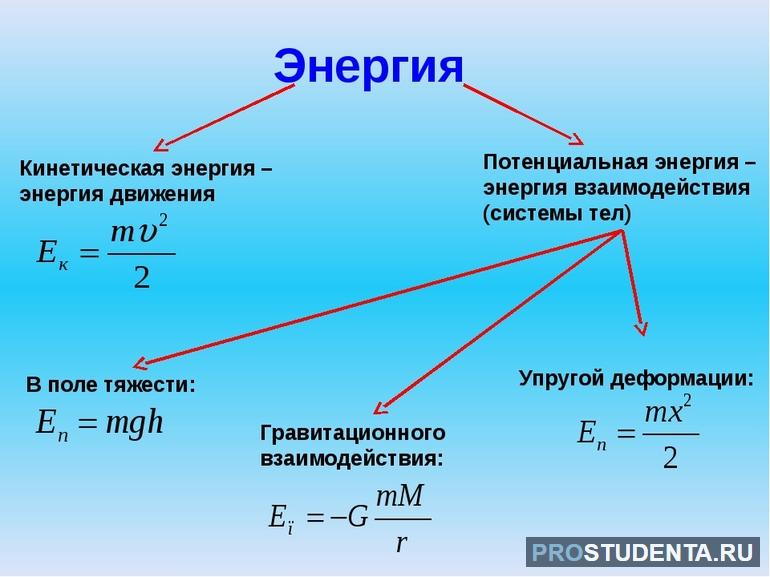
Таким образом, было установлено, что любое тело, если к нему приложить воздействие, сможет совершать работу. Существует два вида энергии:

1. Потенциальная — описывается взаимодействием тел или его частей. Её вычисление зависит от того, какую систему рассматривать. Для вещества, поднятого над землёй, формула для расчёта будет иметь вид: E = m * g * h.
2. Кинетическая — характеризуется значением, которым обладает движущееся тело. Для её расчёта используется выражение: E = (m * V²) / 2.

Получается, что потенциальная энергия — это фактически полезная работа. Например, поднятое тело по наклонной плоскости приобретает потенциал, который потом обеспечивает выполнение действия

. Стоит отметить, что согласно теории относительности Эйнштейна, существует взаимосвязь между массой, энергией и скоростью распространения света в вакууме: E = m * c².

Полная энергия

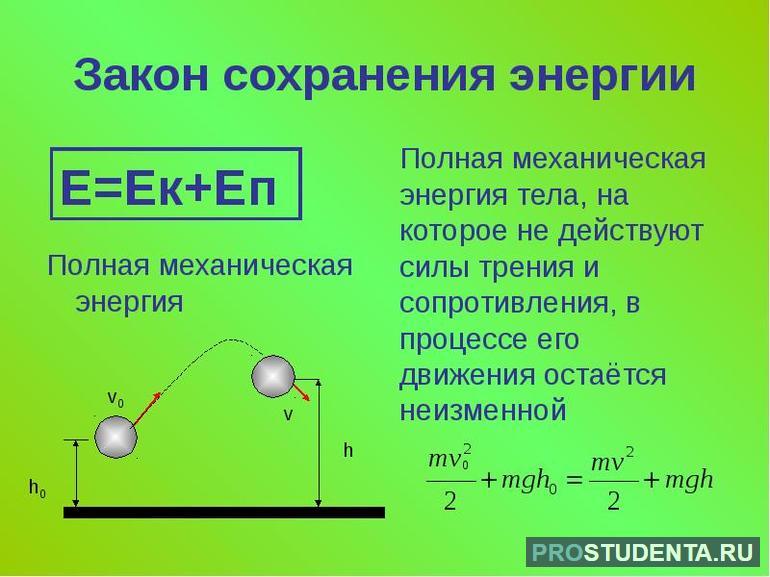
Сформулировать кратко закон сохранения (ЗСЭ) можно так: в замкнутой системе сумма кинетической и потенциальной энергии веществ будет при любом обстоятельстве сохраняться неизменной. Иными словами, при любом взаимодействии тел или выполнении ими работы её значение не может возникнуть из ничего. Энергия не исчезает и не появляется из ничего, а просто переходит из одной формы в другую. Например, электрическая в механическую, химическая в тепловую. По сути, закон отражает закономерность природы, поэтому является фундаментальным принципом.

Можно рассмотреть два явления:

1. Свободное падение. Пусть имеется тело, расположенное на некоторой высотой над землёй, равной h1 в положении 1. При этом оно обладает скоростью V1. Под действием силы тяжести g тело двигается. Траектория его пути будет представлять параболу. На какой-то высоте h2 её скорость будет V2.
2. Имеется сжатая пружина, один конец которой закреплён. Она может толкать тело, которое находится в положении 1, и имеет скорость V1. Так как она сжата, то характеризуется деформацией. Для описания этого процесса нужно вести ось икс, на которой можно обозначить её удлинение как x1. Через некоторое время пружина распрямится, и тело переместится в положение 2. Оно будет описываться скоростью V2 и деформацией x2.

Это два совершенно разных процесса, но которые помогают понять формулу закона сохранения: E = Ep + Ek = const. Первый случай представляет собой систему из двух тел — падающее и Земля. Они взаимодействуют между собой посредством силы тяжести. Во втором случае, кроме толкаемого груза, имеется система, состоящая из пружины и опоры.

Рассматриваемые два процесса замкнутые. В первой системе действует тяжесть, а во второй — упругость. Общее между ними то, что они являются потенциальными силами. Так как суммарная работа всех воздействий, действующих на тело, равняется изменению кинетической энергии, то можно записать: A = Ek2 — Ek1. Это равенство справедливо для любого из рассматриваемых явлений. Но, так как действующие силы потенциальные, работа будет равняться этой энергии, взятой со знаком минус: A = -(Ep2 — Ep1). Для первого случая Ep = m * g * h, а второго: Ep = kx² /2.

Приравняв два выражения, получится равенство: -(Ep2 — Ep1) = Ek2 — Ek1. Отсюда следует, что Ep1 + Ek1 = Ep2 + Ek2. Значит, сумма Ek и Ep в исходном состоянии такая же, как и в конечном. Выражение E = Ep + Ek и получило название «полная механическая энергия».

Закон сохранения

Как оказалось, полная механическая энергия остаётся неизменной. При этом она определяется начальным значением и не изменяется при принятии системой любого состояния вплоть до конечного. Поэтому формула закона сохранения энергии и записывается так: E = Ep + Ek = const, или просто: E = const.

Это правило применимо для случаев, ограниченных следующими свойствами:

• система замкнутая;
• тела взаимодействуют посредством потенциальных сил.

Только при этих условиях выполняется закон. Поэтому правильно формулироваться он будет так: полная механическая энергия замкнутой системы тел, взаимодействующих между собой только потенциальными силами, остаётся неизменной при любых движениях.

Применительно к свободному падению и при действии сил упругости этот закон можно соответственно записать так: (m * g * h1 + (m * v1²)) = (m * g * h2 + (m * v2²)) и (kx1 / 2) +(m * v1²) / 2) = (kx2 / 2) +(m * v2²)). Следует обратить внимание, что первая и вторая запись — уравнение, которое связывает несколько характеристик движения: скорости с высотами и силами упругости или сжатия.

Это подтверждает верность формул, ведь известно, что кинетическая энергия зависит от скорости, а потенциальная — координат. Отсюда следует, что вне зависимости от того, насколько сложной является траектория изменения положения, если известны три из четырёх величин, например, начальная, конечная скорость и высота, то с помощью формулы ЗСЭ можно найти наибольший уровень, которого достигнет тело.

Это удобно, так как не нужно вспоминать кинематику, определять вид перемещения, использовать формулы для проекции. С помощью правила все вычисления можно сделать довольно быстро. Тем более что энергия является скалярной величиной, и нет необходимости строить оси координат. Особенно использование закона актуально при решении задач, связанных с действием переменной силы.

Нужно заметить, что в различных разделах физики существуют свои названия видов энергии. Однако эти имена условные. При переходе из одного типа энергии в другую в системе, соответствующей условиям закона, значение суммы всех присутствующих видов остаётся всегда также постоянной величиной. Поэтому, в отличие от классической механики, закон в других разделах имеет своё название. Так, в электродинамике — теорема Пойнтинга, а в термодинамике — Первое начало.

Решение задач

Практические занятия помогают не только лучше закрепить теоретический материал, но и получить навыки использования знаний для каких-то реальных ситуаций. Обычно они заключаются в решении типовых задач. Вот некоторые из них, рассчитанные на учащихся 10 классов средней школы:

1. Пусть дана наклонная плотность высотой h, с которой скатывается тело. Необходимо определить скорость в нижней точке наклонности. Чтобы решить эту задачу, трением и скольжением нужно пренебречь. В системе действуют только потенциальные силы — тяжести и упругости. Рассматриваемая ситуация замкнутая, так как состоит из тела, Земли и плоскости. Полная энергия в начальном состоянии равняется конечной: E1 = E2. В исходном состоянии Ek = 0, а потенциальная вычисляется как Ep = m * g * h. В конечном же Ep= 0, а Ek = (mv²) / 2 + (I * w²) / 2. Эти два уравнения можно приравнять и выразить V. При этом момент инерции переписать так: I = k * m * r². В результате расчётная формула примет вид: V = √ (2 * g * h) / (1 + k).
2. Груз массой 25 кг висит на шнуре длиной 2,5 метра. На какую наибольшую высоту можно отвести подвес, чтобы он не оборвался. Прочность шнура: Fmax = 550 Н. В такой системе действует сила упругости троса и тяжести груза. В положении, когда тело поднято, будет справедливо равенство: m * g * h = (m * v²) / 2. Отсюда: V² = 2 * g * h. Чтобы найти вес в нижней точке, нужно учитывать силы тяжести и натяжения. В соответствии с законом Ньютона: m * g + Fmax = m * a. Ускорение находится так: a = Vmax² / L. После подстановки и упрощения получится: hmax = L / 2 ((Fmax / m * g) — 1) = 1,5 м.
3. Камень бросили вверх с начальной скоростью 3 м / с. Определить, на какой высоте его Ek = Ep. Сопротивлением воздуха пренебречь. Для того чтобы найти высоту, нужно записать расширенное равенство: m * g * h = (m * V²) / 2. Отсюда: h = V² / (2* g). Скорость тела к этому моменту достигнет значения: V = V — g * t. Значит: h = (v — g * t)² / 2 g. Но, так как: -((2 * v * g * t) / 2 * g) + ((g * t)² / 2) = -h, то: h = v² / ((2 * g)) — h → h = v² / (4 * g) = 9 / 40 = 0,225 м.

   

Таким образом, чтобы правильно решать задачи, нужно знать, как вычисляется кинетическая и потенциальная энергия. Понимать, какие силы действуют в системе, и уметь их правильно описать. При этом во время расчётов необходимо пристальное внимание уделять единицам измерения подставляемых в формулу величин.

Все вычисления нужно выполнять в системе СИ.