Вывод формулы длины медианы правильного треугольника

Знание геометрических свойств различных элементов той или иной фигуры позволяет с легкостью решать практические задачи. Одной из них является определение длины медианы правильного треугольника. Формул для решения этой задачи существует несколько, и каждая из них может быть получена с помощью простых геометрических рассуждений.

Оглавление:

• Характеристика правильного треугольника
• Медиана в геометрии
• Длина Ma для равносторонней фигуры
• Решение задачи

Характеристика правильного треугольника

Прежде чем вывести формулу длины медианы, необходимо рассмотреть фигуру, которая будет изучаться.Правильный треугольник является самым простым и высоко симметричным плоским геометрическим объектом.Состоит он из трех сторон и трех вершин. Для него справедливы следующие свойства:

1. Все три стороны фигуры равны между собой. При решении задач их длина обычно обозначается латинской буквой a. Тогда периметр треугольника будет равен P = 3*a.
2. Три угла фигуры равны между собой и составляют 60 градусов каждый. Это утверждение доказать несложно, если вспомнить, что, во-первых, против равных сторон лежат одинаковые углы, а во-вторых, их сумма должна составлять 180 градусов.
3. Все известные линейные геометрические элементы совпадают друг с другом в равностороннем треугольнике. Это означает, что биссектриса, медиана и высота, которые проведены из одной вершины, лежат на одной прямой. Например, высота не только под прямым углом пересекает противоположную сторону, но и делит ее на две равные части так же, как и угол соответствующей вершины.
4. Точка пересечения высот (медиан, биссектрис) является центром геометрическим, симметрии и масс. Этот факт следует из высокой симметричности рассматриваемого треугольника.
5. Фигура переходит сама в себя за счет вращения вокруг ее барицентра на углы 0, 120, 240 и 360 градусов. Кроме того, разделенная пополам медианой, она переходит сама в себя за счет зеркального отражения относительно указанного элемента.
6. Любые два равносторонних треугольника являются подобными друг другу. Каждый из них представляет собой миниатюрную или увеличенную копию другого.

Геометрические свойства треугольника с равными сторонами изучались со времен философов античной Греции. Ими же получены многие формулы, касающиеся расчетов площади, высоты, геометрического центра и других элементов.

Не только математики интересовались характеристиками этой симметричной фигуры. Так, в 1825 году в военном дневнике Наполеона Бонапарта был обнаружен чертеж, который показывал, что если на сторонах произвольного треугольника достроить равносторонние объекты, а затем, соединить их геометрические центры, то получится новый треугольник с равными сторонами. Это утверждение получило название теоремы Наполеона.

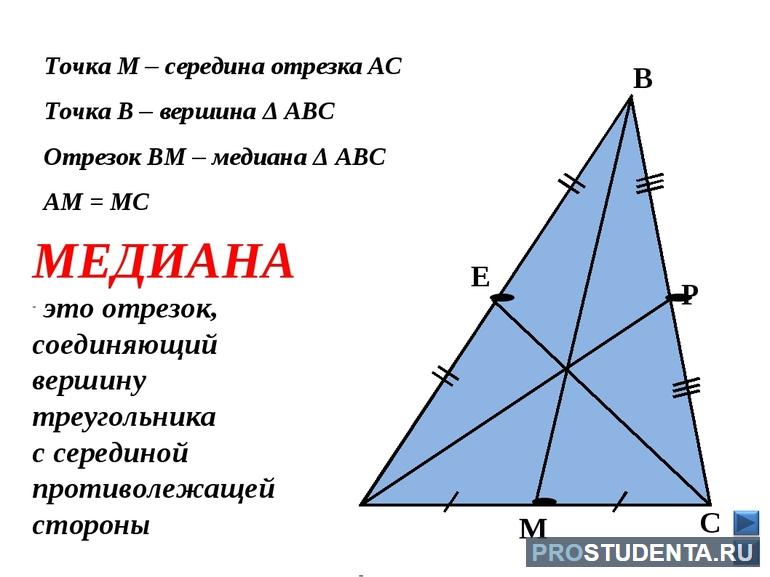
Медиана в геометрии

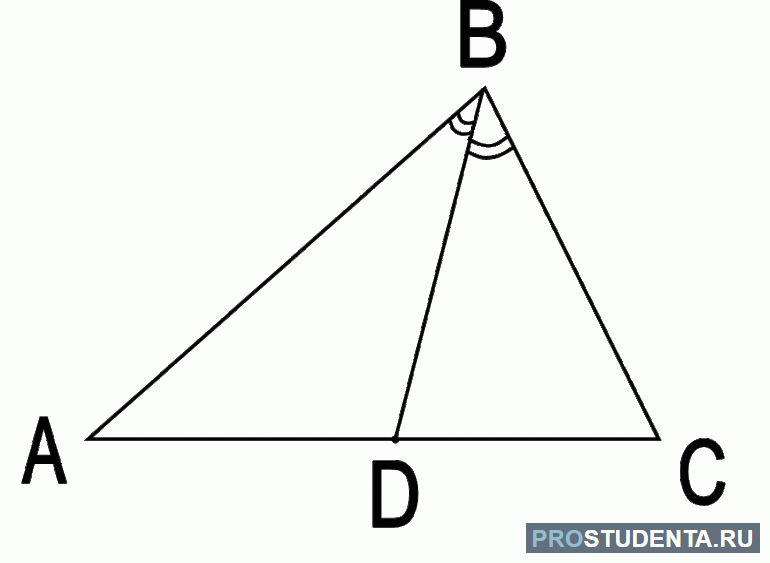
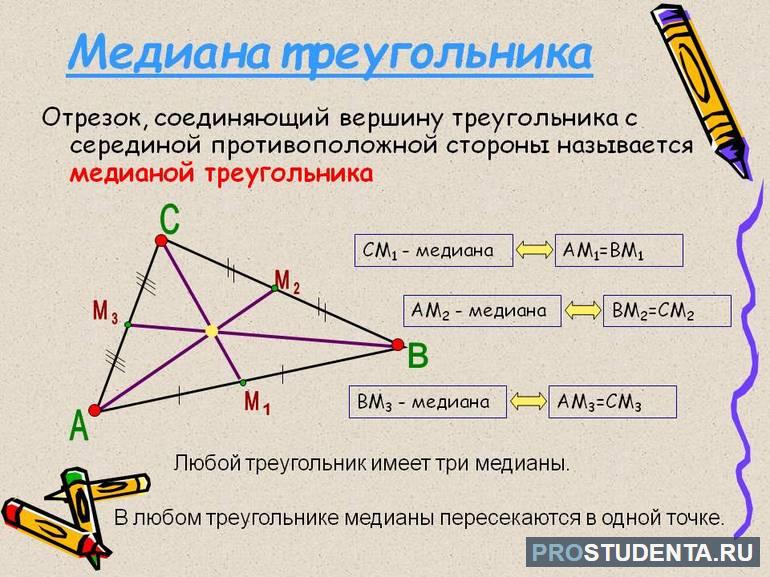
До того как привести вывод формулы медианы треугольника, полезно рассмотреть подробнее этот геометрический элемент. Он представляет собой отрезок, который начинается в вершине фигуры и заканчивается в точке, лежащей на середине противоположной стороны. Таким образом, медиана делит пополам сторону треугольника, к которой она проведена. Следует не путать ее с биссектрисой, которая делит пополам угол при вершине, а не сторону.

Основные свойства элемента

Как и любой геометрический объект, медиана также обладает некоторыми присущими только ей математическими свойствами. Основными из них являются следующие:

1. Рассматриваемый элемент делит пополам любой треугольник так, что образуется две новых фигуры с тремя вершинами каждая. Новые треугольники в общем случае не являются равными или подобными, однако, их площади всегда равны друг другу. Иными словами, медиана делит произвольный треугольник на две одинаковые по площади фигуры.
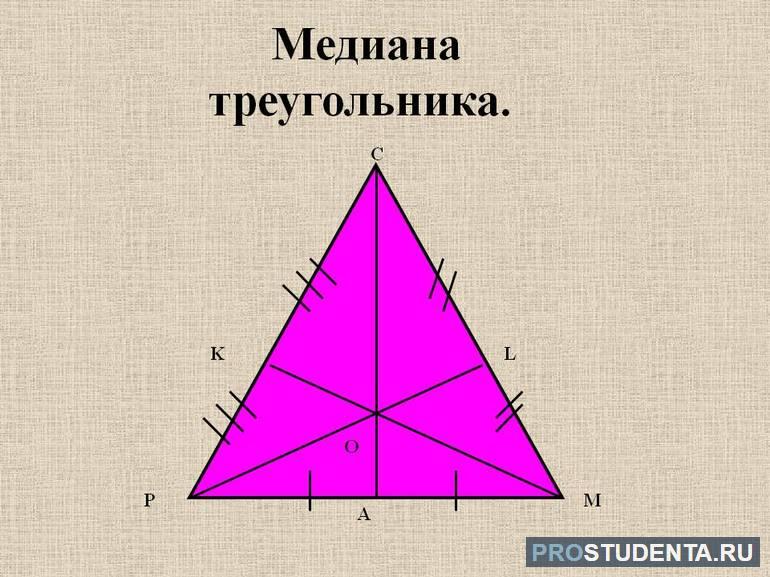
2. Поскольку рассматриваемая фигура имеет три вершины, то внутри нее можно провести только три медианы. Все они будут пересекаться в одной точке, которая является барицентром или центром масс исходного треугольника. Это утверждение справедливо только в том случае, если фигура имеет равномерную плотность.
3. Точка барицентра делит медиану на две части таким образом, что та ее часть, которая ограничивается вершиной треугольника, оказывается всегда в два раза длиннее, чем отрезок, который ограничивает сторона фигуры. Математически это записывается так: AO = 2*OM, где O — барицентр, АМ — медиана.

Две важные формулы

Зная свойства медианы, можно получить несколько формул, которые связывают ее длину со сторонами треугольника. Здесь следует отметить два важных выражения, каждое из которых часто применяется при решении геометрических задач:

1. Связь между длинами трех медиан и сторон треугольника.
2. Теорема Аполлония.

Первая формула выглядит следующим образом:

Ma ² + Mb ² + Mc ² = ¾*(a ² + b ² + c ²).

Здесь Ma, Mb и Mc — длины медиан, опущенных на стороны треугольника a, b и c, соответственно. Это соотношение справедливо всегда, независимо от типа рассматриваемой фигуры (равнобедренный, равносторонний, произвольный).

С помощью теоремы Апполония можно вычислить длину медианы через стороны. Античный греческий философ Аполлоний Пергский в III веке до нашей эры установил, что для произвольного плоского треугольника сумма квадратов двух его сторон равна половине квадрата его третьей стороны плюс удвоенный квадрат соответствующей медианы. Математически следует записать такое выражение:

a ² + b ² = ½*c ² + 2*Mc ².

Здесь видно, что соответствующая медиана Mc опущена именно на сторону c.

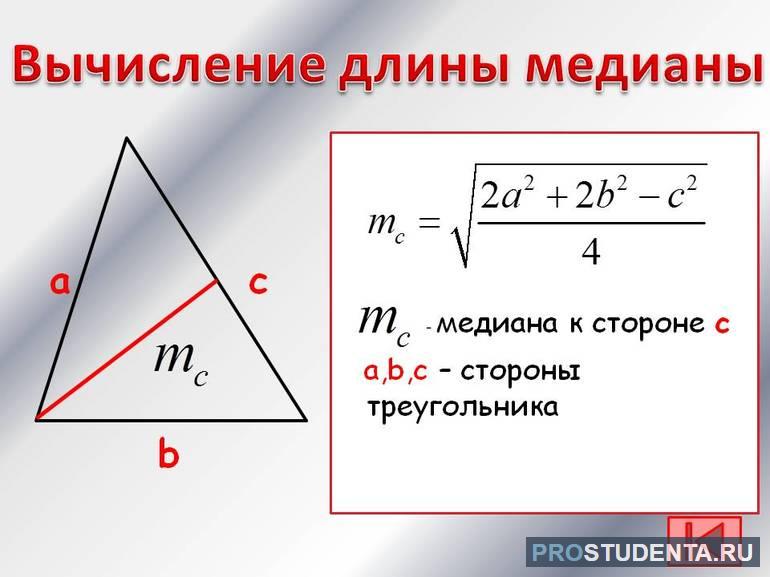
Обе записанные формулы можно с успехом применять при решении сложных геометрических проблем с треугольниками. Например, чтобы получить длину Mc, следует произвести несложные математические преобразования с формулой Аполлония. В результате можно записать следующее полезное равенство:

Mc = ½*(2*(a ² + b ² ) — c ² )^(½).

Оно является искомым для расчета длины рассматриваемого элемента через стороны произвольного треугольника на плоскости. Аналогичные выражения можно записать для отрезков Ma и Mb:

• Ma = ½*(2*(c ² + b ² ) — a ² )^(½);
• Mb = ½*(2*(c ² + a ² ) — b ² )^(½).

Длина Ma для равносторонней фигуры

Благодаря высокой симметрии треугольника с равными сторонами можно применить несколько формул для определения искомого выражения длины его медианы. Поскольку все они равны между собой, то можно ввести единое обозначение для их длины латинской буквой M. В списке приведены способы определения M для рассматриваемого треугольника:

1. Через формулу Ma ² + Mb ² + Mc ² = ¾*(a ² + b ² + c ² ). Это довольно простой способ. Необходимо учесть равенство сторон и длин Ma, Mb и Mc, тогда это выражение преобразуется в следующее простое равенство: 3*M ² = 9/4*a ² . Откуда следует искомая формула: M = 3 ^0,5/2*a.
2. С использованием теоремы Аполлония. Соответствующее выражение для длины медианы произвольного треугольника имеет форму: Ma = ½*(2*(c ² + b ² ) — a ² )^(½). Применяя его к случаю с равносторонней фигурой, получается следующий результат: M = ½*(2*(a ² + a ² ) — a ² )^(½) = 3 ^0,5/2*a.
3. Применяя теорему Пифагора. Предположим, что имеется равносторонний треугольник ABC, AM — его медиана, которая опущена на сторону BC. Поскольку она также является высотой, то фигура AMC будет прямоугольной, где угол при вершине M имеет 90 градусов. В треугольнике AMC отрезок AM — это катет, AC — гипотенуза, MC — второй катет. Согласно теореме Пифагора длина AM равна следующей величине: AM = (AC ² — MC ² )^0,5 = (a ² — (a/2)^2)^0,5 = 3 ^0,5/2*a.
4. Воспользовавшись тригонометрическими выражениями, чтобы вывести формулу длины медианы. Пусть AM — медиана в равностороннем треугольнике ABC. Тогда можно воспользоваться тригонометрическими функциями синуса и косинуса применительно к фигуре AMC или AMB. Для случая косинуса получается следующее выражение: cos (MAC) = AM/AC. Если подставить известные величины, получается: cos (30) = AM/a. Откуда следует искомое выражение: AM = 3 ^0,5/2*a.

Все выводы формулы для медианы в равносторонней фигуре с тремя вершинами приводят к одному и тому же результату: исследуемая характеристика однозначно определяется длиной стороны треугольника. Это утверждение не является удивительным, поскольку рассматривается высоко симметричный геометрический объект на плоскости.

Решение задачи

Лучшим способом закрепления полученных знаний является решение практических задач. Пусть имеются следующие три точки на координатной плоскости:

• A (0;0);
• B (6;0);
• C (3;5).

Они соединены друг с другом отрезками так, что получился треугольник ABC. Необходимо доказать, что он является равносторонним, и найти длину его медианы.

Для решения задачи следует рассчитать все стороны фигуры, используя для этого формулу длины вектора через координаты его конца и начала:

PQ = ((Px — Qx)^2+(Py-Qy)^2)^0,5.

Здесь P (Px; Py) и Q (Qx; Qy) — точки, определяющие начало и конец вектора PQ.

Применяя эту формулу для случая задачи, получается следующий результат:

• AB = ((6 — 0)^2+(0−0)^2)^0,5 = 6;
• BC = ((3 -6)^2+(5−0)^2)^0,5 = 6;
• AC = ((3 — 0)^2+(5−0)^2)^0,5 = 6.

Поскольку три стороны треугольника имеют равную друг другу длину, то он является равносторонним (необходимый и достаточный признак).

Для определения длины M любой из медиан фигуры, воспользуемся простой формулой:

M = 3 ^0,5/2*a = 3 ^0,5/2*6 = 5,196.

Таким образом, из-за высокой симметрии равностороннего треугольника все его медианы равны друг другу и являются одновременно высотами и биссектрисами. Их длины однозначно вычисляются из знания стороны фигуры.