Формула и определение потенциала электростатического поля

Вокруг любой обладающей зарядом микрочастицы появляется энергия электростатического поля. Потенциал этой силы определяется характеристикой, описывающей работу, совершаемой для переноса элементарных частиц. При их взаимодействии происходит изменение материи, которое удобно определять, сравнивая отдельные точки в пространстве. Для разности потенциалов даже ввели специальную величину — напряжение.

Оглавление:

• Общие сведения
• Понятие потенциала
• Напряжённость и потенциал
• Простейшие задачи

Общие сведения

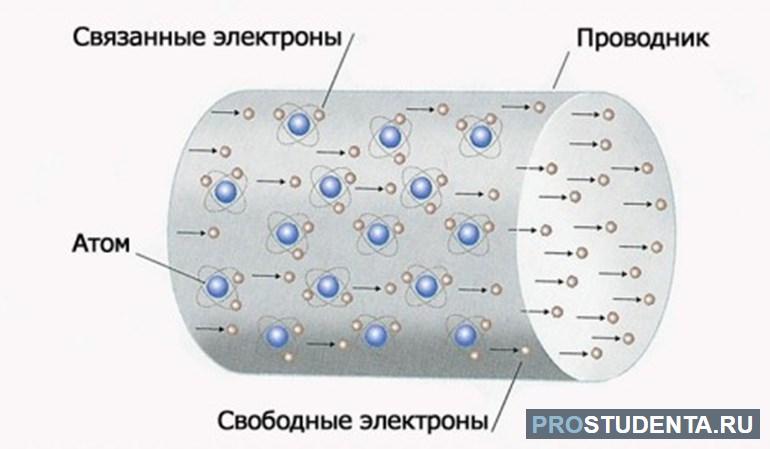
Структура твёрдых веществ определяется строением их кристаллической решётки. Состоит она из набора атомов, ионов или молекул. Вокруг узла движутся заряженные вещества. Самой лёгкой из известных элементарных частиц является электрон. Он участвует во всех электрических процессах, возникающих в теле. Так как атом — электронейтральная частица, то число электронов в нём всегда равняется количеству протонов. Но вместе с тем в теле существуют и свободные частицы. Они не привязаны к атомам и могут перемещаться по кристаллической решётке.

Движение свободных электронов происходит хаотично. При этом они могут сталкиваться с примесями или противоположными им веществами. Многочисленные эксперименты учёных показали, что каждая элементарная частица обладает определённым количеством энергии. Именно она определяет силу взаимодействия между ними. Так, Кулон в 1785 году установил закон, по которому силы влияния двух зарядов друг на друга определяются отношением произведения их энергий и квадратом расстояния между ними.

Фактически физик описал способ нахождения силы притяжения или отталкивания. Этот закон справедлив только для неподвижных зарядов. Но так как сами по себе они существовать не могут, а только когда есть носитель, то правило применимо к элементарным частицам.

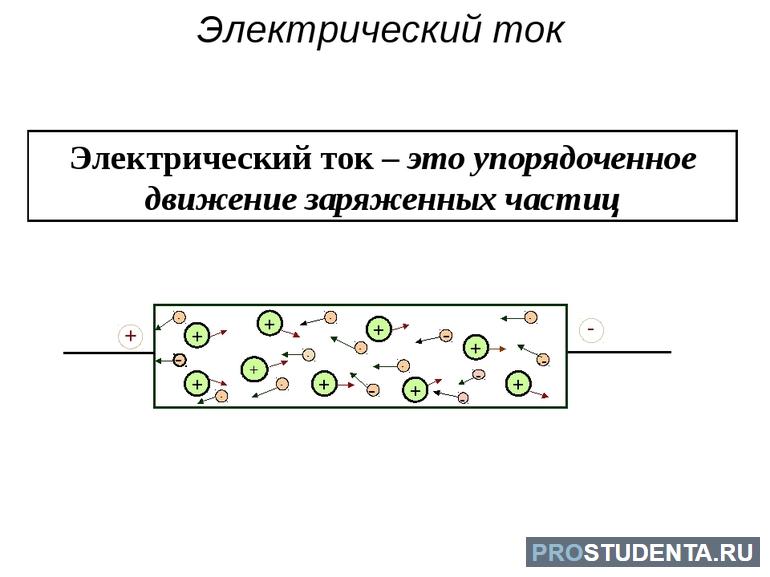
В спокойном положении физическое тело находится в состоянии электрического равновесия. Но если к нему приложена внешняя сила, например, деформация или магнитное поле, хаотичное перемещение электронов меняется на упорядоченное. Возникает электрический ток. Характеризуется он силой, которая определяется работой необходимой для переноса частицы из одной точки тела в другую.

Но если таких сил нет, тело всё равно обладает определённой энергией. Отсюда различают два состояния:

• электростатическое — определяется внутренней энергией свободных частиц;
• электромагнитное — возникающее при упорядоченном движении зарядов.

Энергетической характеристикой электростатического поля служит потенциал. Это скалярная величина, специально введённая для определения энергии неподвижного электрона. То есть является отношением потенциальной работы в постоянном поле к заряду. С помощью потенциала можно численно описать материю поля, затрачиваемую на перемещение заряда из произвольной точки в бесконечность.

Понятие потенциала

Пусть существует электростатическое поле, в котором есть пробный заряд q. Под ним понимают минимальную энергию, которой обладают элементарные частицы. Например, заряд протона или электрона. Его значение принимают равным 1,6 * 10^-19 Кл. Этот заряд перемещается в постоянном внутреннем поле из одной точки в другую. Такое движение вызвано отсутствием пары и электрических связей.

Со стороны электростатической энергии действует сила. Её можно обозначить как Fe. С её помощью выполняется работа A, направленная на изменение положения пробной частицы. Это воздействие не зависит от пути, пройденного электроном, а определяется только начальным и конечным положением. Открытое свойство было названо «консервативностью заряда» или «потенциальностью». Нужно отметить, что только электростатическое поле может характеризоваться этой величиной.

Под потенциальной энергией точечного заряда понимают скалярную функцию в электростатике, описываемую в координатах как Eп = Eп (x, y, z). Отсюда следует, что работа, совершаемая для перемещения частицы, обладающей энергией, будет равняться разности значений функций в начальной и конечной точке положения: A = Eп1 — Eп2. Каждый потенциал будет описываться своей координатой.

Eп может быть определена с точностью до постоянной. Для этого необходимо лишь назначить точку отсчёта. Выбирают её в зависимости от решаемой задачи. Ей может быть потенциал:

• земли;
• бесконечно удалённой точки поля;
• отрицательной пластины конденсатора.

Но чаще для удобства принимают ноль. Так как значение энергии зависит от электростатических сил и величины заряда, то различные пробные частицы в одной точке могут иметь разный потенциал. Чтобы избежать недоразумений, к термину было добавлено слово «электрический».

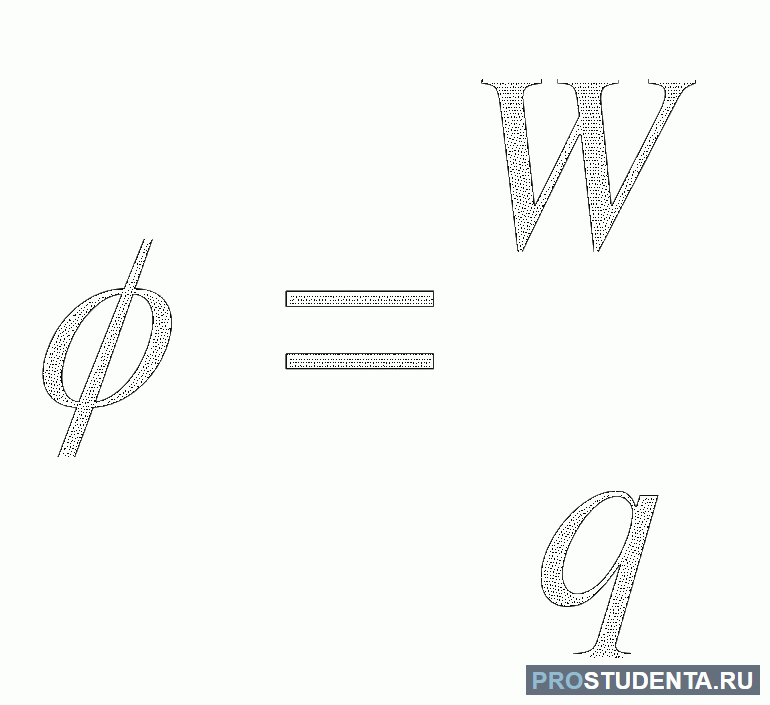
Обозначают эту величину греческой буквой φ (фи). Численно же её находят из отношения: φ = Eп/q. Фактически электрический потенциал является энергетической характеристикой электростатического поля.

В Международной системе измерений принято параметр измерять в вольтах или джоулях, делённых на кулон. Это название для измерения потенциала было выбрано по имени физика Алессандро Вольта, внёсшего огромный вклад в исследование взаимодействия электрических токов и сформулировавшего гипотезу объясняющую магнитные свойства вещества.

Напряжённость и потенциал

Если нет потенциальной энергии, то, естественно, не будет и поля, вызванного этой силой. Электричество может создаваться как положительно заряженной частицей, так и отрицательной. Электростатическая энергия возникает и из совокупности зарядов, имеющих разные знаки. Чтобы можно было определить изменение потенциала, одну из точек считают нулевой. Остальные значения находят относительно этой координаты. Например, в электротехнике за нулевой потенциал принято брать поверхность земли.

Электростатическое поле можно описать с помощью векторной величины напряжённости и скалярной — потенциала. Поэтому между ними должна существовать определённая связь. Если путь перемещения по произвольной траектории обозначить L, то работу на бесконечно малом отрезке можно найти как дифференциал: dA = F * dL. Напряжённость — это величина, пропорциональная силе, действующей на неподвижный заряд и обратно пропорциональна значению энергии частицы: E = F / q. Отсюда следует, что dA = Ei * q * dL. Полная сила, которая воздействует на электрон, выражается формулой Лоренца: F = qE + qV * B, где B — магнитная индукция.

Так как работа, совершаемая при перемещении заряда электростатическим полем, равняется уменьшению потенциальной энергии частицы, изменившей своё положение на dL, то можно записать следующие равенства: dA = - q dφ; Ei * qdL = - qdφ. Отсюда: Ei = - d φ / - dL.

Проекциями напряжённости на оси будут следующие координаты: Ex = -dφ / dx; Ey = -dφ / dx; Ez = -dφ / dx. То есть E = - dφ / dx — dφ / dy — dφ / dz. Градиент этой суммы равен: grad φ = i (dφ / dx) + j (dφ / dy) + k (dφ / dz). Вектор показывает направление возрастания функции. Отсюда связь между потенциалом и напряжённостью будет выглядеть так: E = - grad (φ) = -∇φ, где ∇ - оператор Гамильтона.

Нужно отметить, что разность потенциалов по-другому называется напряжением: φ1 — φ2 = U. Формулу можно представить по-другому: Δφ = ΔW / q. По сути, разница — это приращение потенциала, разница характеризуюется изменением энергии. Отсюда следует, что измеряться напряжение будет в тех же единицах, что и потенциал. Эти выражения действительны лишь при условии, что сторонних сил нет.

Простейшие задачи

Чтобы успешно решать простые задания, связанные с электрическим потенциалом, нужно знать несколько формул. Но при этом нужно уделять пристальное внимание размерности. Вот несколько типовых примеров, предлагаемых к самостоятельной проработке школьникам:

1. Электрические потенциалы двух изолированных проводников, оторванных от пола, равны 110 B и -110 B. Найти работу, которая совершится при переносе заряда 5 * 10^-4 с одного проводника на другой. Под потенциалом понимается, что для первого тела электростатическое поле равняется 110 вольт, а для второго — 110 В. Для решения примера понадобится воспользоваться двумя формулами: U = φ1 — φ2 и E = A / q. Из второго выражения можно определить работу, а вместо напряжения подставить разность потенциалов: A = q * E = q * (φ1 — φ2) = 5 * 10−4 Кл * (110 В + 110В) = 5 * 10−4 Кл * 220 Дж / Кл = 110 * 10−3 Дж.
2. Какую скорость может сообщить электрону, находящемуся в состоянии покоя, ускоряющая разность потенциалов в 1000 вольт. Масса частицы 9,1 * 10^-31 кг. Для решения этой задачи понадобится взять из справочника значение элементарного заряда: e = 1,6 * 10^-19 Кл. Работа, затрачиваемая на движение, определяется как A = q * U = - e * U. Так как заряд отрицательный, то φ2 должно быть больше φ1. Значит: A = e * Δφ. В то же время затрачиваемая энергия равняется ΔW = (mV² / 2) — 0. Остаётся объединить формулы и выразить искомую величину: V = √(2 * e * Δφ) / m = √ (2 * 1,6 * 10^-19 Кл * В) / 9,1 * 10^-31 кг = 1,9 * 10⁷ м / с.
3. Четыре заряда по 40 нКл расположены по углам квадрата со сторонами 4 см. Определить потенциал поля в центре фигуры. Этой серединой в геометрическом теле будет точка пересечения диагоналей. Решая эту задачу, можно опереться на принцип суперпозиции. Он гласит, что потенциал системы будет равен алгебраической сумме полей каждого заряда в отдельности: φ = Σ4φ1. Потенциал точечного заряда можно найти по формуле φ1 = (k * q) / r, где: r — расстояние до точки, где нужно измерить величину. Отсюда следует: φ = 4√2 * K * q / a = 4√2 * 9 * 109 (Н * м2) / Кл * (40 * 10−9 Кл / 4 * 10−2) м = 36 * √2 кВ = 51 кВ.

Таким образом, решать примеры, связанные с потенциалом несложно. Нужно понимать суть величины и уметь анализировать условие задач. Причём все вычисления должны быть выполнены в СИ.