Определение, график и свойства показательной функции

Алгебра и начало анализа — сложная дисциплина, в которую включены графики функций. Свойства показательной позволяют описать не только математические, но и физические процессы.

Оглавление:

• Общие сведения
• Построение графиков
• Дифференцирование и нахождение производной

С ее помощью можно находить множество параметров начиная от обыкновенных задач в университете и заканчивая сложными расчетами выделения энергии при расщеплении атомов вещества.

Общие сведения

Перед рассмотрением показательной функции необходимо начать с базовых понятий и определений. В различных дисциплинах с физико-математическим уклоном встречаются специальные выражения, которые называются формулами. Последние включают в себя переменные, причем одна из них зависит от другой (аргумента). Если подставлять в формулу значения аргумента и выполнять расчеты искомой величины, будут получаться точки.

Точка в прямоугольной системе координат записывается в следующем формате: I(U;R), где U и R - числовые координаты. Иными словами, функцией называется зависимость одного значения от другого. Как правило, ее можно записывать в алгебраической, тригонометрической, степенной, показательной и других формах.

Основным отличием показательной от других зависимостей является наличие известного основания, которое не должно быть равно 0 и возводится в некоторую степень.

Последняя — переменная величина. Функция имеет следующий общий вид: z(m)=N^m (N>0).

Сферы использования

Функцию показательного вида имеет смысл применять при описании процессов, в которых осуществляется стремительный рост некоторой величины.

В зависимости от показателя, она может стремительно возрастать или убывать. Если вместо основания "N" указана экспонента «е», то она стремительно возрастает. Примером показательной функции является формула подсчета энергии, выделяемой при делении ядер радиоактивного элемента: mc(t)=m0*(½)^(t/T).

Ее коэффициенты расшифровываются таким образом:

1. mc(t) — масса радиоактивного вещества, зависящая от времени "t".
2. m0 — масса вещества перед началом эксперимента.
3. Т — значение периода полураспада, который является разным для каждого элемента.

Следовательно, mc(t) зависит не только от времени t, но и от периода T и массы m0. Описание процесса увеличения количества молекул озона (О3) при разряде молний также является примером показательной функции.

Строить ее график довольно просто. Однако перед операцией нужно обратить внимание на ее свойства.

Основные свойства

В физико-математических дисциплинах при неизвестной функции математики рекомендуют строить сначала ее график, а затем определять ее параметры, каковыми являются свойства и утверждения. В противном случае на основании последних можно сразу приступать к графической реализации, которая может быть точной и схематической. Первый тип применяется для анализа процессов, определения параметров для дальнейших расчетов.

График функции рекомендуется строить в декартовой системе координат, являющейся прямоугольной, т. е. ее оси (абсцисс и ординат) образуют угол 90 градусов. Например, в формуле mc(t)=m0*(½)^(t/T) зависимая переменная "mc" — ось ординат, а "t" — абсцисс. Свойства функции значительно упрощают вычисление и построение графика. Для примера необходимо взять самое простое показательное выражение z(m)=N^m (N>0). Для построения графика будут полезны следующие свойства показательной функции:

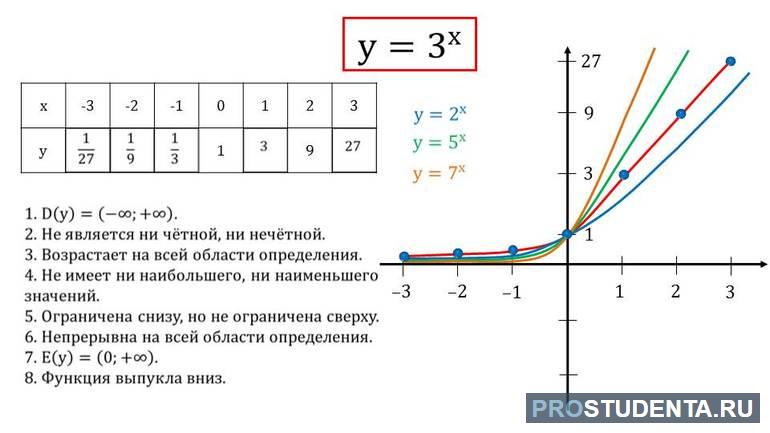
1. Область определения D(z): R (-inf;+inf), где R - действительные числа, "-inf" и "+inf" — плюс и минус бесконечность. На всей D(z) принимает только положительные значения.
2. Область действительных значений (ОДЗ) показательной функции — все значения переменной, не превращающие D(z) в пустое множество) E(z): (0;+inf).
3. Максимумы и минимумы не существуют.
4. Не является четной и нечетной (общий вид).
5. Непериодична.
6. Пересекает ось ординат только в одной точке: (0;1).
7. Нулей нет, т. е. при любом значении аргумента функция не обращается в 0.
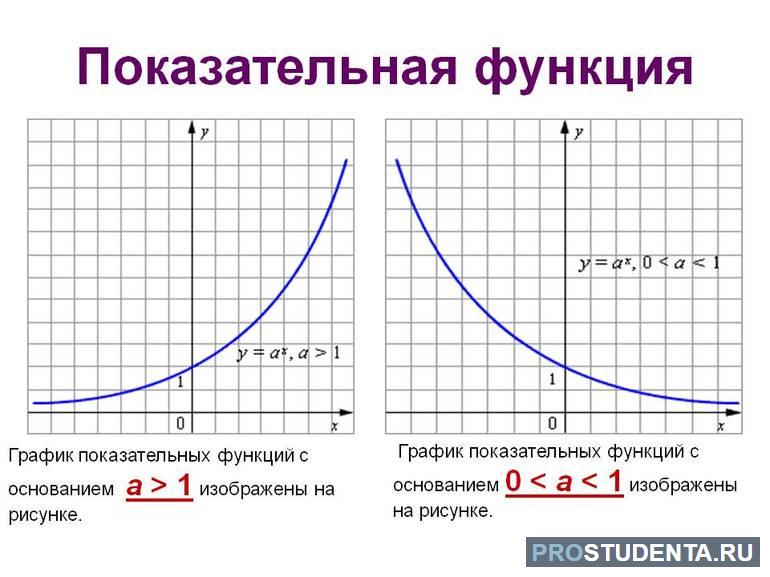
8. Убывает при N<0, а возрастает при значении основания больше 0 (N>0).
9. При N=0 и m<0 является пустым множеством.
10. При отрицательном показателе (m<0) соотношение имеет вид: N^m = 1 / (N^|m|), |y| — модуль аргумента.
11. N^0=1.
12. N^(m+k)=(N^m)(N^k).
13. (N^m)^k=N^(mk).
14. (NS)^m=(N^m)(S^m).
15. (N/S)^m=(N^m)/(S^m), где S не равно 0.
16. N^(m/k)=[N^m]^(1/k)=[N^(1/k)]^m, , где к не равно 0.
17. N^(log (m)|n)=m.
18. N^m=[S^(log(m)|S)]^m=S^[mlog(m)|S)].
19. Если S = e, то тогда показательная функция выражается через логарифм натурального типа: N^m = e^(mln(N)).

Этих свойств будет достаточно для построения графика. Математики рекомендуют разобрать доказательство некоторых из них, чтобы иметь общее представление об их выведении.

Доказательства утверждений

Утверждения необходимы для построения графиков и решения различных задач. Каждое из свойств получено математическим путем. Можно доказать третье свойство, и найти минимум и максимум (экстремумов). Для этого применить алгоритм:

1. Найти производную: [N^m]'=N^m(ln(N)).
2. Вычислить точки, в которых она не существует: при m=0 (N=0), m<0 (N=0) и N<0.
3. Приравнять производную к нулю для нахождения стационарных точек: [N^m]'=0.
4. Уравнение N^m(ln(N)) не имеет решения, поскольку N^m не принимает нулевое значение. Следовательно, экстремумов нет.

Чтобы произвести проверку на четность, математики рекомендуют воспользоваться соответствующим соотношением, имеющим вид: z(-m)=z(m), т. е. N^(-m)=1/|N^m|.

Из тождества видно, что z(-m) не равно z(m). Следовательно, функция не является четной.

Проверка на нечетность производится по формуле: z(-m)=-z(m), т. е. N^(-m)=1/|N^m| (не является нечетной).

Шестое свойство доказывается методом подстановки независимой величины, т. е. z(m)=N^m=N^0=1. Следовательно, искомая точка имеет координаты (0;1).

Построение графиков

Для построения графиков рассматриваются 5 отдельных случаев. К ним относятся:

1. N>0.
2. 0<m<1.
3. N<0 и m>0.
4. N=0 и m>0.
5. N=1 и m>0.

Чтобы построить график, нужно определить параметр точности (схематический или точный). При первом необходимо знать только свойства. Если нужны точные значения величин, без таблицы зависимости значения функции от аргумента не обойтись.

Минимальное количество элементов таблицы - 5. После этого производится расчет посредством подстановки аргумента в формулу функции, и отмечается точка в декартовой системе координат.

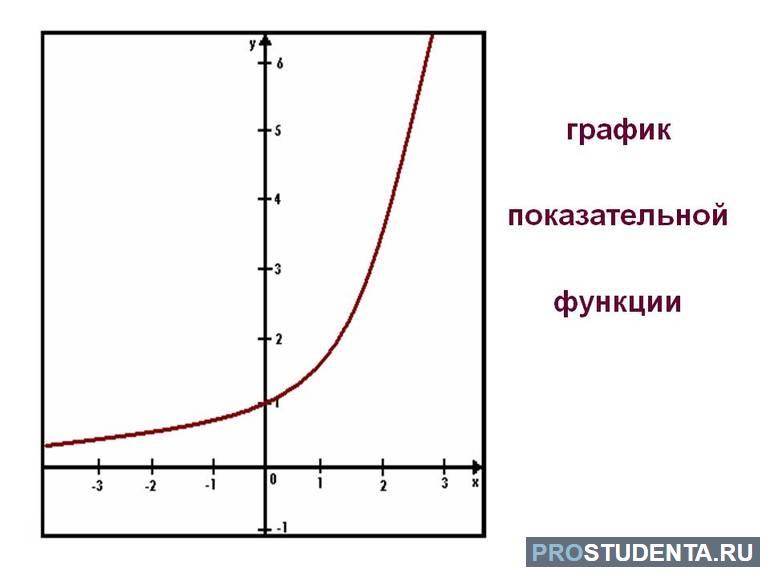
Специалисты рекомендуют обратить внимание на графическое представление. Оно не должно содержать много правок, не допускается прописывать на шкалах все значения. График функции, кроме ручного, можно построить посредством программного обеспечения (онлайн-калькуляторов и специализированных веб-сервисов). На начальном этапе составляется таблица (рисунок 1). Для примера следует рассмотреть тождество z=2^m.

Таблица 1. Зависимость значения от аргумента (z = 2^m).

По таблице отмечаются точки, которые потом соединяются. В результате должна получиться кривая, проходящая через (0;1). Она стремительно возрастает. Если m>0 и 0<N<1, графическое изображение не будет круто расти по сравнению с предыдущим графиком. При N<0 и m>0 график начинает убывать.

При основании N=0 функция уже не является показательной. Это происходит из-за несоблюдения условия из определения. Если N эквивалентно 1, ее также нельзя отнести к этому виду.

Дифференцирование и нахождение производной

Существует определенный тип задач, в которых требуется найти дифференциал и производную искомой степенной функции.

Некоторые учащиеся часто путают эти 2 термина. Отличие между ними следует разобрать на примере: найти дифференциал z = 2^(3m).

Для этого нужно воспользоваться следующим алгоритмом:

1. Выразить 2 через основание "e": 2 = e^(ln2).
2. Подставить в искомое выражение: z = 2^(3m)=e^[ln(2*3m]=e^[2ln(3m)].
3. Дать обозначение новой переменной p=[2ln(3y)]: z=e^p.
4. Найти производную: z'=[e^р]'=e^р.
5. Записать дифференциал: dz/dm=(dz/dp)(dp/dm)=(e^p)3ln(2) = [2^(3n)]*2ln(3m).

Производная находится на 4 шаге, а дифференциал на пятом. Отличие заключается в методике нахождения, поскольку производная является промежуточным значением.

Таким образом, для построения графика показательной функции следует знать ее свойства, которые будут также полезны при решении различных задач, нахождении параметров величин и описания физических процессов.