Закон сохранения и превращения энергии с примерами

Закон сохранения и изменения энергии в механике: в изолированной системе сумма всех видов энергии постоянна.

Оглавление:

• Полная механическая энергия
• Законы сохранения и превращения энергии
• Общий принцип сохранения энергии

Этот закон относится к определенной группе правил в физике. С одним из них мы уже встречались ранее, а именно – с законом сохранения импульса. В механике есть еще один закон — сохранения углового момента.

Полная механическая энергия

Сумма потенциальной и кинетической энергии тела называется полной механической энергией: E=Ep+Ek. Но тело может иметь одновременно и потенциальную, и кинетическую E. Например, космический корабль, парящий на небольшой высоте h со скоростью v, имеет Ep=mgh и Еk =(mv ² )/2. Таким образом, E корабля составит: ΔE=mgh+(mv ² )/2.

Если пилот включит двигатели, то создастся сила, которая выполнит работу A. Эта сила может привести к изменению как высоты полета, так и скорости. Таким образом, за счет этой работы происходит увеличение ΔEp и прирост ΔEk. Сумма этих двух видов E будет равна ΔE и равна работе A. То же самое относится к любому телу и любой системе тел, в которой действуют только консервативные (потенциальные) силы.

Итак, у нас есть уравнение: ΔE=ΔEp+ΔEk. Это уравнение является выражением очень важной закономерности, встречающейся во всех механических явлениях, в которых силами сопротивления и трения можно пренебречь. Работа внешних сил равна изменению полной механической энергии системы.

Предположим теперь, что система изолирована, то есть на нее не действуют внешние силы, в ней не совершается работа. Тогда A = 0 и прирост E системы равен нулю (хотя в ней могут происходить различные процессы), то есть: ΔE=E2−E1=0. Отсюда следует, что E1=E2=const.

Полная механическая E системы тогда постоянна. Символами E1 и E2 отмечают здесь механическую E системы, соответственно, перед рассматриваемым процессом и после него.

Законы сохранения и превращения энергии

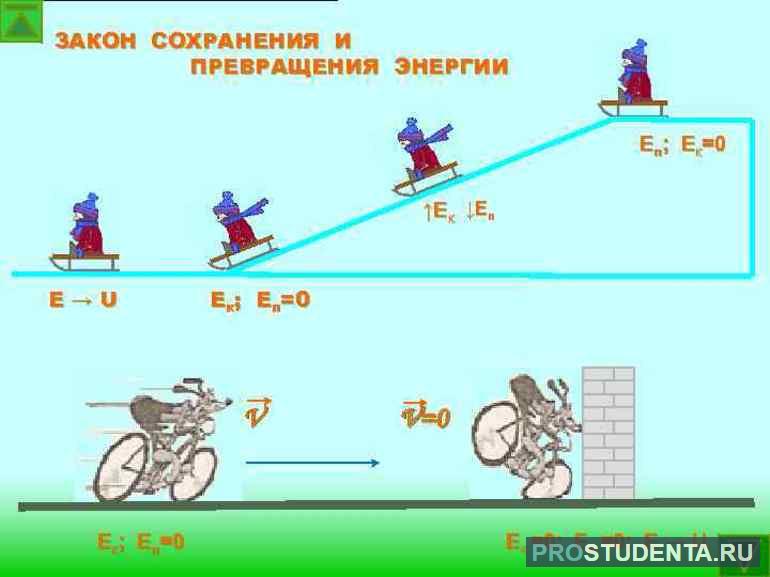
ΔE=Ep+Ek=const. Полная механическая энергия изолированной системы является постоянной (сохраняется). Закон превращения энергии: ΔE=Ep1+Ek1=Ep2+Ek2;

Энергия в замкнутой системе может переходить из кинетической в потенциальную, но при этом полная механическая E остаётся неизменной.

Стоит привести примеры превращения механической энергии во внутреннюю, сохранения E, работы E в замкнутой системе.

Пример 1

Упругий шар поднимают с земли на высоту h, затем отпускают. Какова будет его энергия в разных точках относительно земли?

Решение: На высоте h Ep = mgh, Ek =0. Под действием силы тяжести шар падает, его кинетическая E растет, потенциальная уменьшается. При подъеме шара его кинетическая энергия уменьшается, потенциальная увеличивается. Определить E шара можно, используя формулы Ek и Ep. На высоте h1 Ep = mgh1. Для того чтобы определить Ek, необходимо для начала найти скорость: v = at. t — время, его можно найти, используя формулу:

• h = v0+(gt ^2)/2, если шар падает;
• h = v0-(gt ^2)/2, если шар поднимается.

Пример 2

Тело соскальзывает без трения по наклонной плоскости высотой h. Сколько составит скорость тела v у основания плоскости?

Решение: Помимо силы тяжести, которая является консервативной, на тело также действует сила реакции опоры. Однако не нужно решать, является ли эта сила консервативной, — достаточно заметить, что она перпендикулярна направлению смещения тела. Это означает, что сила тяжести компенсируется силой реакции опоры (по третьему закону Ньютона) и что она не влияет на преобразования E в этой системе.

Полная энергия тела на вершине составляет E1=Ep+0=mgh, а у основания E2=0+Еk=(mv ²)/2. При сравнении этих двух величин можно вывести формулу для конечной скорости. Поскольку дано, что трения нет, то: mg = ma, ускорение a будет равняться g. v=√(2gh);

Как видно, конечная скорость тела зависит только от высоты, с которой тело соскользнуло, и не зависит от угла наклона.

Выводы:

• у вершины тело имеет только потенциальную энергию,
• у основания - только кинетическую.

Пример 3

Тело сползает равномерно, а затем преодолевает «дьявольскую петлю» радиусом R. Без учета трения рассчитайте, с какой высоты h тело должно начинать движение, чтобы оно не отрывалось от петли даже в самой высокой точке.

Решение: Тело, сползая вниз по склону, набирает скорость и может преодолеть «дьявольскую петлю». Для этого должны соблюдаться некоторые условия. Если скорость тела в пиковой точке петли будет достаточно большой, то центробежная сила (прижимания тела к петле) F0=(mv ²)/R будет как минимум равна силе тяжести P=mg, отделяющей его от петли. Отсюда получаем условие: (mv ²)/R=mg; v^2=gR.

С другой стороны, из закона сохранения E следует, что потенциальная E тела на вершине равна Ep=mgh — энергии в пиковой точке петли. Эта последняя энергия состоит из потенциальной энергии mg ⋅ 2R и кинетической энергии (mv ²)/2. Итак, есть уравнение: mgh=mg ⋅ 2R+(mv ²)/2. Отсюда h=2R+(v ²)/2g. После подстановки здесь v²: h≥5R /2.

Видно, что это условие не зависит от ускорения свободного падения g. Следовательно, такое же условие будет действовать на Луне и на каждой планете.

Пример 4

Брусок соскальзывает без трения по стенкам полого сосуда, выполненного в форме параболы в уравнении y=cx ². Какая будет зависимость потенциальной энергии Ep(x) тела от координаты х?

Решение: потенциальная E относительно дна вырезки составляет Ep(x)=mgh, где высота h в процессе проскальзывания тела составляет y, таким образом, Ep(x)=mgy. Так как y=cx2, поэтому Ep(x)=mgcx ^2.

Кривая потенциальной энергии является параболой типа: Y=Kx ², где K=mgc является постоянным коэффициентом. Форма этой кривой потенциальной энергии такая же, как и форма сосуда, в которой перемещается брусок.

Легко прийти к общему выводу, что для сосуда любой формы форма кривой потенциальной E такая же, как и форма сосуда. Схожесть этих двух понятий заставила использовать понятие потенциальной ямы (или потенциальной скважины) в разных случаях, когда мы имеем дело с движением тел в силовом поле (а не только в гравитации). Это понятие очень полезно и применяется для многих физических вопросов, например, в атомной физике.

Пример 5

При ударе молотом по бруску E будет передаваться в системе молот — брусок, причем это яркий пример превращения механической E во внутреннюю. Молот совершает работу при ударе и передает часть E бруску, который, в свою очередь, нагревается.

Общий принцип сохранения энергии

Принцип сохранения механической энергии соблюдается строго в том случае, если силы сопротивления и трения отсутствуют или настолько малы, что ими можно пренебречь. В противном случае в процессе часть механической энергии будет потеряна. Но действительно ли это так?

Нет, потому что именно эту часть энергии мы находим в выделяющемся тепле. В общем случае механическая Е может превращаться в различные формы. Например, потенциальная Е падающей воды может двигать турбину, производящую электрический ток. В этом случае механическая E превращается в электрическую. Известно много разных форм энергии: механическая, электрическая, электромагнитная, ядерная и т. д.

Рассмотрим изолированную систему тела, в которой могут происходить превращения одной формы E в другую. Пусть система изолирована таким образом, что никакая форма E не ускользает и не проникает в систему. Получается, что тогда общая сумма всех возможных форм E постоянна. Это означает, что она не может исчезнуть или получиться из ничего. В результете бесчисленных экспериментов, открытий и ​​научных наблюдений была подтверждена вера в неприкосновенность этого закона.

Все это имеет принципиальное значение в химии и физике, поскольку вытекает из основных свойств пространства и времени. Закон сохранения энергии вытекает из основного свойства времени, которое заключается в том, что время в пустом пространстве течет всегда одинаково, никогда не ускоряется и не замедляется.

А также закон сохранения импульса вытекает из аналогичного свойства пространства, называемого неоднородностью пространства.