Определение равномерного движения, формулы скорости и пути

Движение различных объектов окружает человека с самого рождения. Перемещение автомобиля по асфальтированной дороге, полет самолета, бег атлета на спортивных соревнованиях, вращение планеты Земля вокруг своей звезды — это лишь малая доля примеров изменения пространственного положения объектов. Для решения задач по физике нужно знать, что такое равномерное движение.

Оглавление:

• Пространственная система координат
• Понятие механического движения
• Физические величины
• Виды перемещения в пространстве
• Равномерное изменение положения
• Пример решения задачи

Пространственная система координат

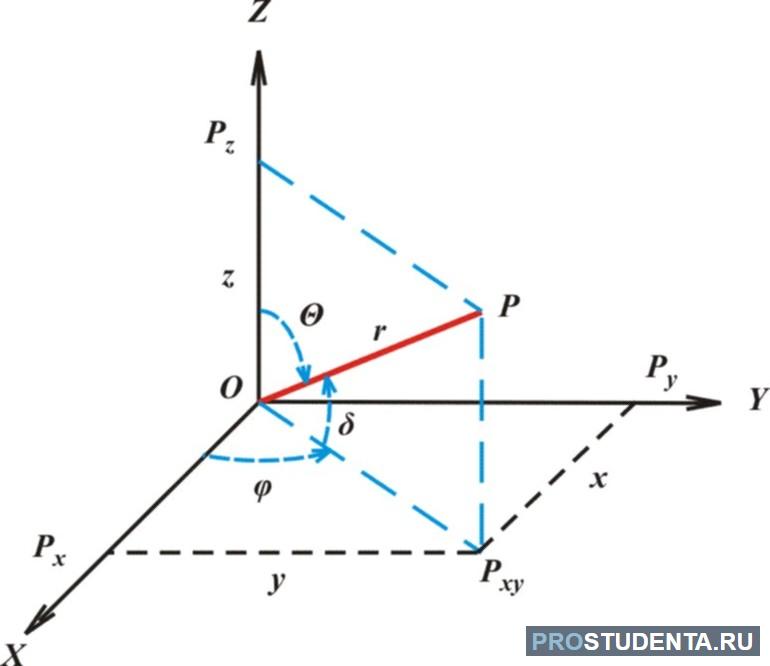
Состояние Вселенной в общем случае можно представить в виде функции, зависящей от четырех координат. Три координаты описывают положение тела в пространстве, четвертая — это время, которое характеризует последовательность событий. Пространственные координаты в большинстве задач по физике и геометрии удобно представлять в виде прямоугольной декартовой системы. Эта система является совокупностью трех пересекающихся под углом 90 градусов осей, на каждой из которых выбран единичный вектор.

Положение любой точки в декартовой системе координат можно математически представить в виде суммы целых длин единичных векторов для каждой из трех осей. Благодаря этой системе можно легко описывать изменение положения тел в пространстве.

Понятие механического движения

Любое изменение пространственных координат тела во времени принято называть механическим движением. Школьников слово «механический» может вводить в заблуждение, поскольку оно связано с каким-либо механизмом. Для некоторых из них перемещение автомобиля или мотоциклиста — это движение механическое, а бег животного или полет птицы уже не вписывается в эту категорию.

При рассмотрении типа изменения пространственных координат физика сосредотачивает свое внимание на законах этого изменения, а также на силах, которые его вызвали. При этом она не исследует природу объекта, поэтому любое движение считается механическим.

Физические величины

Путь, время, скорость и ускорение — это 4 главные величины, которые характеризуют пространственное изменение координат объектов. Каждая из них относится к одной из двух групп:

• векторная;
• скалярная.

Путь и время — это скаляры, для их определения достаточно знать начальное и конечное состояние тела. Например, объект, перед тем как начать движение, имел координату x0, в момент завершения своего перемещения его координата стала равной x1. Численное значение пройденного пути S в этом случае определяется просто:

S = x1 — x0.

Скорость и ускорение — характеристики векторные. Это означает, что для их полного определения недостаточно знать только начальное и конечное положение тела. Обе величины определяют характер самого движения.

По определению, скорость v — это быстрота изменения координат объекта в пространстве, ускорение a — это быстрота изменения самой скорости. Величина v для всякого типа перемещения тел направлена всегда вдоль траектории (воображаемая линия, вдоль которой объект движется). Ускорение a совершенно не связано ни с величиной v, ни с траекторией. Направление вектора a однозначно определяется результирующей суммой сил, действующих на изучаемое тело в движении.

Виды перемещения в пространстве

Примеры механического движения можно встретить в живом и неживом мире, в технике, в микромасштабе и в масштабах галактики. Несмотря на огромное разнообразие, физика выделяет всего 2 группы видов перемещения тел:

• равномерное;
• неравномерное.

В первую группу входят все явления, перемещение тел для которых происходит без изменения абсолютного значения скорости на протяжении всего пути. Соответственно, вторая группа описывает виды движения, в процессе которых скорость, так или иначе изменяется по модулю.

Во время равномерного перемещения объектов в пространстве ускорение не всегда равно нулю. В процессе неравномерного движения величина a всегда отлична от нуля. Примером, относящимся к первой группе, является перемещение автомобиля с заданной скоростью по дороге. Падение камня с некоторой высоты на поверхность земли — это пример неравномерного движения с ускорением свободного падения.

Равномерное изменение положения

Этот тип перемещения в пространстве рассматривают в начальных классах школ, поскольку он наиболее простой в изучении и понимании смысла физических формул. Тем не менее часто школьники отождествляют равномерное и прямолинейное перемещение, что неправильно.

По прямой линии

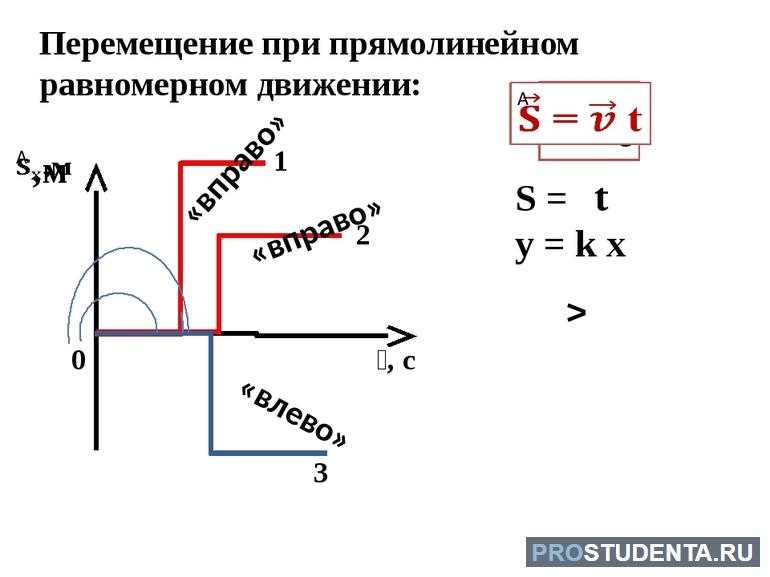
Самолет, летящий в облаках с постоянной скоростью по воображаемой прямой линии, в первом приближении можно полагать хорошим примером равномерного прямолинейного движения. Для физического описания подобных перемещений используют 2 скалярные величины — пройденный путь S и время t, и одну векторную характеристику — скорость v. Формула равномерного движения по прямой имеет следующий вид:

S = v*t.

Левая и правая часть выражения имеет размерность длины, которая в международной системе СИ выражается в метрах (м). Часто S также выражают в миллиметрах, сантиметрах или километрах. Поскольку t имеется размерность времени (секунды, минуты, часы), величина v выражается в единицах длины по отношению к единицам времени, то есть в метрах в секунду (м/с), километрах в час (км/ч) и т. д.

Формулу пути S можно легко переписать, чтобы определить скорость равномерного движения v или время t:

v = S/t; t = S/v.

Кривая траектория

Планета Земля вращается вокруг Солнца в космическом пространстве. Является ли ее движение равномерным? Да. Является ли оно прямолинейным? Нет. Если бы наблюдатель мог со стороны посмотреть на движение Земли, то увидел бы, что она перемещается по окружности с огромной скоростью (приблизительно 30 км/с). В каждый момент времени вектор скорости планеты изменяется за счет действия гравитационного притяжения Солнца, однако абсолютная величина скорости не испытывает каких-либо изменений. По этой причине продолжительность года на Земле является постоянной величиной.

Движение тел по кривым траекториям, в процессе которого ускорение изменяет только направление скорости, а не ее величину, в физике принято называть равномерным криволинейным перемещением. Чаще всего рассматривают круговое движение, для которого вводят важную характеристику — центростремительное ускорение ac. Эта величина всегда направлена к центру окружности, а ее модуль вычисляется по следующей формуле:

ac = v ² /r.

Здесь r — радиус круговой траектории, v ² — квадрат скорости.

Угловые характеристики и период

Равномерное движение по окружности удобно описывать не линейными, а угловыми физическими величинами, то есть угловой скоростью w и углом перемещения Q. Величина w измеряется в радианах в секунду (рад/с), Q — в радианах. Поскольку полная окружность представляет собой 2*pi радиан (pi = 3,14 — число пи), угловые характеристики через их линейные аналоги можно рассчитать по следующим формулам:

w = v/r; Q = S/r.

Еще одна важная величина, которую необходимо знать для полного описания равномерного движения по окружности — период T. Он представляет собой время, которое затрачивает тело для совершения полного оборота по замкнутой траектории. Вычисляется период следующим образом:

T = 2*pi/w.

Период обращения Земли вокруг своей звезды равен продолжительности года, то есть 365 дней и 6 часов. Для удобства времяисчисления каждый четвертый год на планете на 1 день длиннее предыдущих трех.

Пример решения задачи

Мотоциклисту необходимо попасть из пункта A в пункт C, совершая при этом остановку в пункте B на 1 час. Известно, что между пунктами A и B мотоциклист двигался с некоторой постоянной средней скоростью v1. Между пунктами B и C его движение также было равномерным, но уже со скоростью v2, которая на 20% была больше, чем v1. Какое расстояние преодолел мотоциклист, если известно, что затраченное на переезд время составило 5 часов, скорость v1 была равна 50 км/ч, и расстояние между B и С он преодолел в 1,5 раза быстрее, чем путь между A и B.

Пусть на переезды между пунктами A-B и B-C мотоциклист затратил время t1 и t2, соответственно. Справедливо следующее выражение:

t1 + 1 + t2 = 5.

Здесь 1 час в левой части равенства отражает время отдыха в пункте B. Чтобы найти t1 и t2, следует обратиться к условию задачи. Известно, что величина t2 в 1,5 раза меньше, чем t1:

t1 = 1,5*t2.

Из двух записанных выражений следует, что t1 = 2,4 часа, t2 = 1,6 часа.

Прохождение пути определяется как сумма дистанций между AB и BC. Длина траектории S, то есть расстояние между A и C, рассчитывается по формуле для равномерного движения:

S = v1*t1 + v2*t2.

Согласно условию v1 = 50 км/ч, и v2 = 1,2*v1, значит, v2 = 60 км/ч. Все определенные величины, подставленные в формулу для S, приводят к следующему результату:

S = 50*2,4 + 60*1,6 = 216 км.

Траектория движения мотоциклиста между пунктами A и C необязательно должна быть прямолинейной. Для нахождения пройденного расстояния S важно, чтобы на каждом отрезке пути он двигался с некоторой постоянной по модулю скоростью.