Правило деления обыкновенных дробей для 5 класса

В различных дисциплинах с физико-математическим уклоном встречается операция упрощения выражений. Иногда последние представлены в виде обыкновенных дробей. Правила деления и умножения дробных тождеств нужно знать, чтобы не совершать ошибок при вычислениях. Специалисты рекомендуют изучить теорию, а потом перейти к ее практическому применению.

Оглавление:

• Общие сведения
• Подготовительные операции
• Деление и умножение дробей

Общие сведения

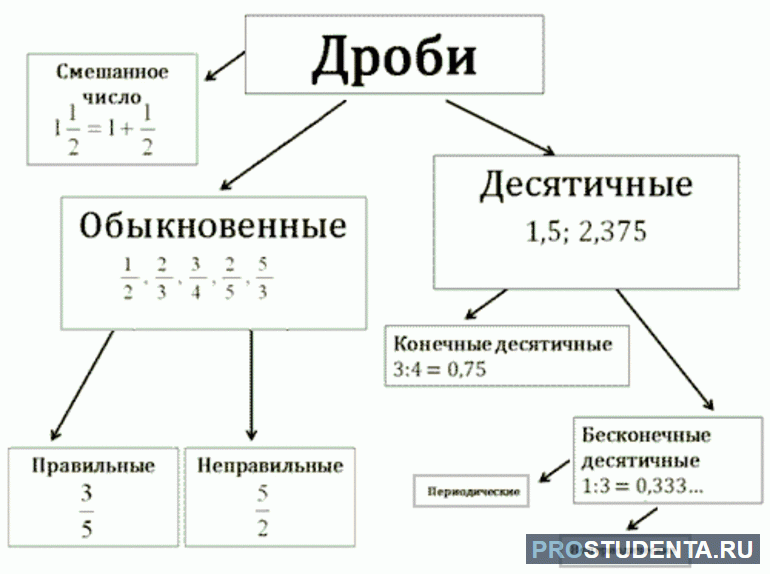
Многие начинающие математики путают правила работы с обыкновенными выражениями, поскольку при делении забывают «переворачивать» делитель. Некоторые не отличают обыкновенное дробное выражение от десятичного. Кроме того, следует также знать правила деления числа на определенное значение. Итак, дроби бывают только двух типов:

1. Обыкновенными (правильными и неправильными).
2. Десятичными (конечными и бесконечными).

Правильная — дробное выражение, у которого числитель меньше знаменателя, а у неправильного — числитель больше знаменателя (пример 2/3 и 7/3). У конечной десятичной дробной величины после запятой находится определенное количество знаков. Если же она является бесконечной, то делится на 2 типа: бесконечная периодическая (0,85 (3)) и непериодическая (1,56471238971235). Первая отличается от второй повторяющимися знаками, которые следует выделять круглыми скобками 0,(36) через определенный промежуток.

Обыкновенное дробное выражение записывается в десятичной форме. Кроме того, существует и обратное утверждение: любую десятичную дробь возможно записать в виде обыкновенной. Существует еще определенный вид дробных чисел, называющихся смешанными. Они состоят из целой части и обыкновенной дроби, т. е. 4 (½). Деление дробей в 5 классе требует некоторых подготовительных операций.

Подготовительные операции

Чтобы разделить одну дробную величину на другую, требуется произвести некоторые действия. Для этого следует руководствоваться правилом: любое смешанное число должно быть преобразовано в неправильную обыкновенную дробь. В этом случае математики рекомендуют воспользоваться следующим алгоритмом:

1. Записать величину: 12 (2/5).
2. Умножить знаменатель на целую часть, а затем прибавить числитель: 12*5+2=62.
3. Записать результат в виде неправильной дробной величины: 62/5.

Обратную операцию по преобразованию неправильной дроби в смешанное число математики рекомендуют выполнять на завершающих этапах вычисления. Выполняется конвертация по такой методике:

1. Записывается искомая величина: 62/5.
2. Выделяется целая часть при делении: 12.
3. От числителя искомого значения отнимается произведение знаменателя на величину, полученную во 2 пункте: 62−12*5=62−60=2.
4. Записывается конечный результат: 12 (2/5).

Правило деления целого числа на дробь: произвести преобразование целого в дробь деление на 1, т. е. 4=4/1. Следует также рассмотреть признаки делимости чисел. Они помогут правильно вычислять выражения и быстро сократить полученный результат. К ним относятся:

1. На 1 делится любое число без остатка.
2. Если последняя цифра является четной, величину возможно разделить на 2.
3. Величина делится на 3, когда сумма ее цифр делится на это значение.
4. Число делится на 4, когда сумма двух крайних справа цифр можно разделить на последнее.
5. Если величина заканчивается на 5 или 0, значит, 5 является ее делителем.
6. Деление на 6 выполняется нацело в том случае, когда выполняются второе и третье правила.
7. Чтобы разделить величину на 7, нужно от произведения всех цифр, не затрагивая последнюю, отнять двойной разряд единиц. В этом случае результат должен делиться на семерку.
8. При делении на 8 нужно соблюдение второго и четвертого условий.
9. Если число делится на 9, то на нее должна делиться и сумма цифр, составляющих искомую величину.

Математики рекомендуют заготовить специальные карточки на плотной бумаге или в виде презентаций на компьютере. Для этих целей может подойти программа PowerPoint, входящая в расширенный выпуск Microsoft Office.

Описанных рекомендаций будет достаточно, чтобы выполнить деление обыкновенных дробей. Правило, которое используется при этой операции, включает в себя преобразование величин, выполнение вычислений, а затем приведение к общему виду.

Деление и умножение дробей

При делении обыкновенных дробей рекомендуется на начальных этапах использовать алгоритм. Последний не понадобится, когда учащийся выполняет операцию большое количество раз. Методика имеет следующий вид:

1. Записать 2 дроби: 3 (2/5) и 12 (2/5).
2. Преобразовать их в неправильные дробные выражения: (5*3+2)/5=17/5 и (12*5+2)/5=62/5.
3. Развернуть делитель (вторую дробь) и сменить знак деления «:» на противоположный (*), сократив на «5»: (17/5)*(5/62)=17/62.
4. Упростить результат при необходимости.

Деление целого значения на дробь выполняется по такому же алгоритму. При умножении обыкновенных дробных величин нет необходимости их переворачивать. Методика является очень простой и сводится к перемножению числителей и знаменателей, а затем результат упрощается.

Таким образом, для выполнения операций деления и умножения двух обыкновенных дробей рекомендуется изучить признаки делимости, алгоритмы и определения, а затем переходить к практике.