Формулы площади прямоугольного треугольника через катеты

При решении задач по геометрии очень часто возникает необходимость вычислить площадь прямоугольного треугольника через катеты. В интернете можно найти много информации на эту тему, но не всегда она соответствует действительности, поскольку некоторые авторы не являются экспертами в физико-математическом направлении. Они упускают алгоритмы правильного выполнения заданий, что приводит к некачественному обучению.

Оглавление:

• Теорема Пифагора
• Нахождение площади
• Простая задача
• Сложное задание

Общая информация

Прямоугольный треугольник — разновидность фигуры, один из углов которой эквивалентен градусной мере в 90 градусов. У него, как и другого вида, есть 3 стороны, имеющие названия катеты и гипотенуза. Именно 2 катета образуют прямой угол. Их соединяет гипотенуза. Последняя всегда больше любого катета.

Сумма углов фигуры эквивалентна 180 градусам. Из этого утверждения следует, что сумма углов между гипотенузой и катетами всегда будет равна 90, поскольку 180 - 90 = 90.

Фигура обладает некоторыми параметрами:

1. P: периметром.
2. S: площадью.
3. H: высотой.
4. M: медианой.
5. B: биссектрисой.

Первая величина (P) — алгебраическая сумма всех сторон фигуры. Площадь — величина фигуры, определяющая ее размерность. При нахождении S в литературе по геометрии можно встретить понятие «полупериметр», которое обозначает половину значения Р. Высота фигуры — перпендикуляр, опускающийся всегда из некоторой вершины на противоположную сторону. У него существует и другое название — проекция. Она всегда опускается из прямого угла на гипотенузу, поскольку из других вершин треугольника нет смысла ее опускать, т. к. отрезок совпадает с катетами.

Медиана — отрезок, проведенный из любой вершины к середине противоположной стороны. Биссектриса — прямая, проходящая через заданную вершину и делящая угол при ней на 2 равных значения. Биссектриса может быть и отрезком, проведенным к противоположной стороне. Необязательно она может пересекать центр гипотенузы или катета.

При решении задач на нахождение площади прямоугольного треугольника необходимо знать теорему, показывающую взаимосвязь сторон этой фигуры.

Теорема Пифагора

Впервые связь между сторонами прямоугольного треугольника («Δ») установил древнегреческий ученый по имени Пифагор. Формулировка его утверждения следующая: в египетском «Δ» (прямоугольном) квадрат большей стороны (гипотенузы) эквивалентен алгебраической сумме квадратов двух других сторон (катетов).

Из теоремы следует, что условие будет выполняться только для прямоугольного треугольника. Этот прием используется при решении задач на идентификацию фигуры. Если катеты равны v и u соответственно, а гипотенуза - t, то утверждение записывается в виде формулы: v^2 + u^2 = t^2.

Чтобы доказать теорему, нужно построить «Δ» с прямым углом, со следующими сторонами: DE = v, DF = u и EF = t. Первые 2 параметра — катеты, последний — гипотенуза. Далее требуется провести высоту к стороне EF из вершины прямого угла ∠D. При этом образуется два прямых угла ∠FOD = ∠EOD = 90. Прямоугольные «Δ», образованные высотой, подобны по 2 сторонам и прямому углу. На основании последнего утверждения можно вывести такие соотношения:

1. v / t = OE / v.
2. u / t = FO / u.

После получения выражений нужно избавиться от черты дроби. Для этого требуется перемножить элементы по свойству пропорции: v ² = t * OE и u ² = t * FO. Затем следует сложить 2 соотношения: v^2 + u^2 = t * (OE + FO) = t * t = t^2.

Утверждение Пифагора доказано. Однако это всего одно доказательство, поскольку ученые насчитывают более 70 версий.

Нахождение площади

Наиболее простой метод позволяет находить площадь прямоугольного треугольника через значения катетов.

На основании этого составляются другие соотношения, позволяющие вычислить искомую величину при неизвестной стороне, меньшей гипотенузы.

Необходимо рассматривать фигуру с параметрами, описанными при доказательстве теоремы Пифагора, а именно: катетами DE = v, DF = u и гипотенузой EF = t.

Основные соотношения для нахождения S при следующих известных значениях:

1. Два катета: S = vt / 2.
2. Гипотенуза и один из углов: S = (t^2 * sin(∠F) * cos(∠E)) / 2 = (t^2 * sin(2∠F)) / 4 = (t^2 * sin(2∠E)) / 4.
3. Катет и прилегающий к нему ∠: S = (v^2 * tg(∠E)) / 2 = (u^2 * tg(∠F)) / 2.
4. В прямоугольный треугольник вписана окружность с радиусом R, которая делит гипотенузу t на отрезки t1 и t2: S = R(R + t) = t1 * t2.

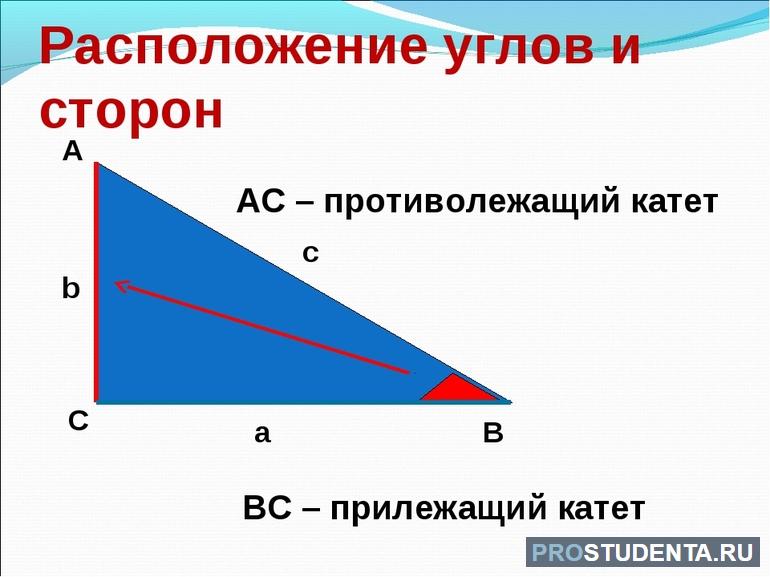
Необходимо отметить, что тригонометрическая функция sin называется синусом угла. Она равна отношению противоположного катета к линейной мере гипотенузы (длине).

Косинус (cos) — величина, которая может находиться из отношения прилежащего катета к t.

Первая формула используется также и при определении площади прямоугольника или квадрата. Как известно, эти фигуры имеют прямые углы. Диагональ делит квадрат (прямоугольник) на 2 «Δ» с прямыми углами. Следовательно, результирующее значение площади состоит из численных значений «Δ», т. е. S = S1 + S2 = (vt / 2) + (vt / 2) = 2vt / 2 = vt.

Пример решения

При решении задач по геометрии необходимо руководствоваться алгоритмом, рекомендуемым специалистами. Суть его состоит в следующем:

1. Внимательно несколько раз прочитать условие и кратко его записать.
2. Записать основную формулу нахождения S.
3. Схематически изобразить фигуру (если есть в этом необходимость).
4. Определить недостающие величины посредством формул.
5. Подставить соотношения из 4 пункта во 2. Можно вычислить отдельно каждую величину.
6. Найти искомый результат.

Далее нужно разобрать решение задач при помощи алгоритма, которые делятся на простые и сложные.

К первому типу относятся задания на одно или два действия, а ко второму — несколько действий. В условиях последних указано минимальное количество известных параметров.

Простая задача

Необходимо найти S прямоугольника с исходными данными: большая сторона 4, а диагональ 5. Решать следует по алгоритму. Пусть диагональ LN = 5, а сторона KN = 4. Последняя больше, чем другая LK.

Основная формула, по которой требуется найти S: S = KN * LK. В соотношении неизвестна величина LK. Чтобы ее найти, следует воспользоваться теоремой Пифагора: (KN)^2 + (LK)^2 = (LN)^2. Если выразить LK, получится выражение, в которое следует подставить числовые значения: LK = [(LN)^2 - (KN)^2]^(1/2) = [25 - 16]^(1/2) = [9]^(1/2) = 3 (ед). Далее следует подставить последнюю величину в результирующую формулу: S = 4 * 3 = 12 (ед^2).

Следует обратить внимание на единицу измерения, указанную в скобках. Если в условии она не дана, пишется «ед». Следующая задача немного сложнее.

Сложное задание

Требуется найти S прямоугольника, в котором известна диагональ (5 м), а также одна сторона больше другой на 1 м.

Краткая запись условия: диагональ LM = 5 м, стороны — KN = LK + 1. Чтобы найти S, необходимо знать катеты треугольника. Их значения неизвестны, но они связаны таким соотношением: KN = LK + 1.

В этом случае следует ввести обозначения: KN = f и KL = f - 1. Воспользовавшись утверждением Пифагора, можно получить такое уравнение: f^2 + (f - 1)^2 = 25.

Решается оно следующим образом:

1. Раскрываются скобки: f^2 + f^2 - 2f + 1 = 25.
2. Приводятся подобные слагаемые: 2f^2 - 2f + 1 = 25.
3. Находится дискриминант: D = 4 + 12 = 16 (2 корня).
4. Вычисляются корни уравнения: f1 = (2 - 4) / 2 = -1 (не подходит) и f2 = (2 + 4) / 2 = 3 (м).
5. Рассчитывается площадь прямоугольника: S = 4 * 3 =12 (м^2).

Значение f1 = -1 не подходит, поскольку сторона не может иметь отрицательное значение. Второе значение является истинным.

Таким образом, необходимо уметь находить S прямоугольного треугольника, поскольку формулы помогут решать не только простые задачи, но и более сложные.