Закон Гука - определение и формула
Всё, что происходит в природе, основывается на действии различных сил – закон Гука является тому подтверждением. Это одно из основополагающих явлений науки.
Оглавление:
Этот процесс является определяющим звеном процессов сжатия, изгибов, растяжения и других видоизменений материалов различных структур.
Разберёмся, в чем же заключается этот закон, как можно применить правило Гука на практике, и всегда ли оно выполняется.
Определение и формула закона Гука
Давно люди пытались объяснить происхождение явлений сжатия и растяжения. Отсутствие знаний являлось причиной накопления экспериментальных данных. Собственно, свою теорему английский испытатель Гук открыл из своих наблюдений и опытов. Только позже, после смерти ученого, современники назовут выведенную им аксиому – законом Гука.

Исследователь заметил, что при каждом упругом воздействии на объект появляется сила, которая возвращает его в исходную форму. Это и послужило началом экспериментов.
Аксиома Гука гласит:
При очень маленьких упругих воздействиях создается сила, пропорциональная изменению объекта, но противоположного знака по абсолютной величине перемещения его частиц.
Математически это определение можно записать следующим образом:
Fx = Fупр = -k * x,
где в левой части указывается:
сила, действующая на тело;
x – перемещение тела (м);
k – коэффициент деформации, зависящий от свойств объекта.
Единица измерения, как и любой другой силы, является Ньютон.
Кстати, k еще называют жёсткостью тела, она измеряется в H/м. Жесткость обусловлена не внешними параметрами объекта, а зависит от его материала.
Правда, стоит учесть, что его закон справедлив только для упругих деформаций.
Сила упругости
Формулировка основывается на определении силы упругости. В чем же заключается ее отличие от других воздействий на тело?
На самом деле, сила упругости может возникать в любой точке тела при его упругой деформации. Что понимается под таким воздействием? Это изменение формы тела, при котором объект через определенный период времени возвращается в исходный вид.
А это в свою очередь происходит из-за молекулярного воздействия частиц: при любой деформации происходит изменение расстояния между молекулами объекта, а кулоновские силы притяжения или отталкивания стремятся вернуть тело в исходное положение.
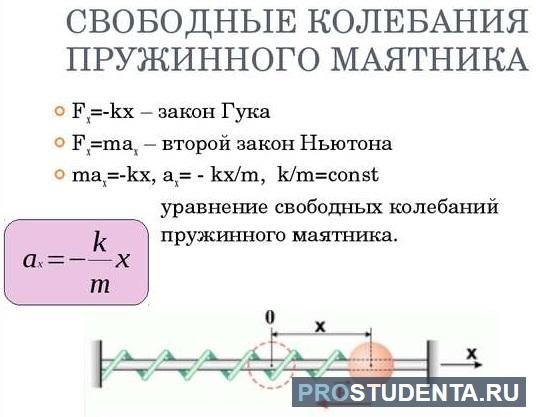
Самая простая модель, демонстрирующая действие сил упругости, является пружинным маятником.
Какая формула выражает аксиому, установленную ученым в этом случае?
Тут аксиома Гука запишется в виде:
ε = α * S,
где ε – относительное удлинение тела (его величина равна отношению удлинения к перемещению);
α – коэффициент пропорциональности (обратно пропорционален модулю Юнга Е);
S – механическое напряжение объекта (его величина равна отношению силы упругости к площади сечения тела).
Учитывая вышесказанное, уравнение можно записать так:
Δx / x = Fупр / E * S,
где Δx – максимальный сдвиг при деформации.
Стоит преобразовать данное выражение, тогда получим следующее:
Fупр = (E * S / x) Δx= k * Δx.
Поскольку сила упругости противоположна внешнему воздействию, то кратко закон читается таким образом:
Fупр = - k * Δx.
В нем не зря упомянуты малые по величине деформации: при них Δx ̴ x, следовательно, Fупр = - k * x.
При каких условиях выполняется закон Гука
А теперь посмотрим, каковы границы применимости этого выражения, и в каких условиях оно вообще выполняется.
Следует знать, что основным условием является:
s = E * e,
где слева в уравнении находится напряжение, возникающее при деформации, а в правой части модуль Юнга и удлинение.
Причем, E зависит от характеристик частиц объекта, но не от его параметров формы, а второй множитель берется по модулю.

В целом аксиома Гука справедлива для многих ситуаций.
Так, при упругом изгибе пружины, лежащей на двух опорах, математическая запись теоремы выглядит следующим образом:
Fупр = -m * g
Fупр = -k * x
В иных ситуациях (при кручении, различных маятниках и других деформирующих процессах) аналогично записывается воздействие сил на объект.
Как применить закон упругой деформации на практике
Этот закон (обобщенный для многих ситуаций) является базовым в динамике и статике тел, поэтому его применимость осуществляется в областях, где необходимо проводить расчет жесткости и напряжения деформации объектов.

В первую очередь, правило Гука необходимо применять в строительстве и технике. Так, рабочие должны точно знать, какой максимальный груз может поднять башенный кран или какую нагрузку выдержит фундамент будущего здания.
Ни один из поездов не обходится без деформации растяжения и сжатия, поэтому закон Гука справедлив и для этих ситуаций. Кроме того, механизм и принцип действия любых динамометров, которыми снабжены некоторые части технического оборудования, также основываются на этом замечательном законе.
Закон Гука выполняется во всех объектах, являющихся аналогами модели «пружинный маятник».

В обычной жизни, дома, можно видеть применимость этого закона в пружинах некоторых механизмов.
Таким образом, закон Гука применим во многих сферах жизни человека. Он является одним из базовых явлений, на которых держится существование всей жизни на планете.
Заключение
Подводя итоги, следует отметить, что закон Гука – универсальный помощник в задачах с решениями по деформации объектов не только в студенческих книжках по сопромату, но и в различных инженерных областях.
Именно эти простые задания помогают ученым и мастерам создавать новые технические модели, необходимые в условиях современного технического прогресса.


Ещё никто не комментировал эту статью. Оставьте комментарий первым!