Формулы сокращённого умножения (ФСУ): таблица и применение

Одной из первых тем, изучаемых в курсе алгебры, являются формулы сокращённого умножения. В 7 классе они применяются в самых простых ситуациях, где требуется распознать в выражении одну из формул и выполнить разложение многочлена на множители или, наоборот, быстро возвести сумму или разность в квадрат или куб. В дальнейшем ФСУ используют для быстрого решения неравенств и уравнений и даже для вычисления некоторых числовых выражений без калькулятора.

Оглавление:

• Как выглядит список формул
• Применение ФСУ для решения уравнений
• Примеры задач для 7−8 класса

Как выглядит список формул

Существует 7 основных формул, позволяющих быстро осуществить перемножение многочленов в скобках.

Иногда в этот список также включается разложение для четвёртой степени, которое следует из представленных тождеств и имеет вид:

a⁴ - b⁴ = (a — b)(a + b)(a² + b²).

Все равенства имеют пару (сумма — разность), кроме разности квадратов. Для суммы квадратов формула не приводится.

Остальные равенства легко запоминаются:

1. Разница между квадратом суммы и разности заключается в знаке перед удвоенным произведением величин.
2. В случае с суммой и разностью кубов в (a ± b) знак совпадает со знаком (a3±b3). Второй сомножитель — так называемый неполный квадрат, поскольку он напоминает квадратный трёхчлен, возникающий после раскрытия скобок в квадрате суммы или разности. Здесь в ситуации с суммой появляется знак минуса перед ab; в противном случае знак заменяется на +.
3. В кубе суммы все знаки положительные; в случае с разностью появляются минусы перед 3a²b и b³.

Следует помнить, что ФСУ работают в любом случае и для любых величин a и b: это могут быть как произвольные числа, так и целые выражения.

В ситуации, если вдруг не получается вспомнить, какой знак стоит в формуле перед тем или иным слагаемым, можно раскрыть скобки и получить тот же результат, что и после использования формулы. Например, если проблема возникла при применении ФСУ куба разности, нужно записать исходное выражение и поочерёдно выполнить умножение:

(a — b)³ = (a — b)(a — b)(a — b) = (a² - ab — ab + b²)(a — b) = a³ - a²b — a²b + ab² - a²b + ab² + ab² - b³ = a³ - 3a²b + 3ab² - b³.

В результате после приведения всех подобных членов был получен такой же многочлен, как и в таблице. Такие же манипуляции можно проводить и со всеми остальными ФСУ.

Применение ФСУ для решения уравнений

К примеру, нужно решить уравнение, содержащее многочлен 3 степени:

x³ + 3x² + 3x + 1 = 0.

В школьной программе не рассматриваются универсальные приёмы для решения кубических уравнений, и подобные задания чаще всего решаются более простыми методами (например, разложением на множители). Если заметить, что левая часть тождества напоминает куб суммы, то уравнение можно записать в более простом виде:

(x + 1)³ = 0.

Корень такого уравнения вычисляется устно: x = -1.

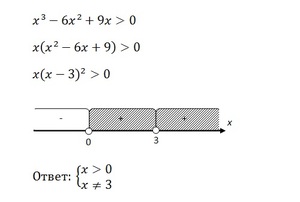
Аналогичным способом решаются неравенства. Для примера можно решить неравенство x³ - 6x² + 9x > 0.

В первую очередь необходимо разложить выражение на множители. Вначале нужно вынести за скобку x. После этого следует обратить внимание, что выражение в скобках можно преобразовать в квадрат разности.

Затем необходимо найти точки, в которых выражение принимает нулевые значения, и отметить их на числовой прямой. В конкретном случае это будут 0 и 3. Затем методом интервалов определить, в каких промежутках x будет соответствовать условию неравенства.

ФСУ могут оказаться полезными при выполнении некоторых расчётов без помощи калькулятора:

703² - 203² = (703 + 203)(703 — 203) = 906 ∙ 500 = 453000.

Кроме того, раскладывая выражения на множители, можно легко выполнять сокращение дробей и упрощение различных алгебраических выражений.

Примеры задач для 7−8 класса

В заключение разберём и решим два задания на применение формул сокращённого умножения по алгебре.

Задача 1. Упростить выражение:

(m + 3)² + (3m + 1)(3m — 1) — 2m (5m + 3).

Решение. В условии задания требуется упростить выражение, т. е. раскрыть скобки, выполнить действия умножения и возведения в степень, а также привести все подобные слагаемые. Условно разделим выражение на три части (по числу слагаемых) и поочерёдно раскроем скобки, применяя ФСУ там, где это возможно.

• (m + 3)² = m² + 6m + 9 (квадрат суммы);
• (3m + 1)(3m — 1) = 9m² - 1 (разность квадратов);
• В последнем слагаемом необходимо выполнить перемножение: 2m (5m + 3) = 10m² + 6m.

Подставим полученные результаты в исходное выражение:

(m² + 6m + 9) + (9m² - 1) — (10m² + 6m).

С учётом знаков раскроем скобки и приведём подобные слагаемые:

m² + 6m + 9 + 9m² 1 — 10m² - 6m = 8.

Задача 2. Решить уравнение, содержащее неизвестное k в 5 степени:

k⁵ + 4k⁴ + 4k³ - 4k² - 4k = k³.

Решение. В этом случае необходимо воспользоваться ФСУ и методом группировки. Нужно перенести последнее и предпоследнее слагаемое в правую часть тождества.

k⁵ + 4k⁴ + 4k³ = k³ + 4k² + 4k.

Из правой и из левой части выносится общий множитель (k² + 4k +4):

k³(k² + 4k + 4) = k (k² + 4k + 4).

Всё переносится в левую часть уравнения, чтобы в правой остался 0:

k³(k² + 4k + 4) — k (k² + 4k + 4) = 0.

Снова необходимо вынести общий множитель:

(k³ - k)(k² + 4k + 4) = 0.

Из первого полученного сомножителя можно вынести k. По формуле краткого умножения второй множитель будет тождественно равен (k + 2)²:

k (k² - 1)(k + 2)² = 0.

Использование формулы разности квадратов:

k (k — 1)(k + 1)(k + 2)² = 0.

Поскольку произведение равно 0, если хотя бы один из его множителей нулевой, найти все корни уравнения не составит труда:

1. k = 0;
2. k — 1 = 0; k = 1;
3. k + 1 = 0; k = -1;
4. (k + 2)² = 0; k = -2.

На основании наглядных примеров можно понять, как запомнить формулы, их отличия, а также решить несколько практических задач с применением ФСУ. Задачи простые, и при их выполнении не должно возникнуть никаких сложностей.