Что такое трапеция: свойства четырёхугольника, теоремы и формулы

В курсе геометрии за 8-й класс подразумевается изучение свойств и признаков выпуклых четырёхугольников. К ним относятся параллелограммы, частными случаями которых являются квадраты, прямоугольники и ромбы, и трапеции. И если решение задач на различные вариации параллелограмма чаще всего не вызывает сильных затруднений, то разобраться, какой четырёхугольник называется трапецией, несколько сложнее.

Оглавление:

• Основные свойства элементов
• Вычисление периметра и площади
• Вписанная и описанная окружность
• Частные случаи

Определение и виды

В отличие от других четырёхугольников, изучаемых в школьной программе, трапецией принято называть такую фигуру, две противоположные стороны которой параллельны друг другу, а две другие — нет. Существует и другое определение: это четырёхугольник с парой сторон, которые не равны между собой и параллельны.

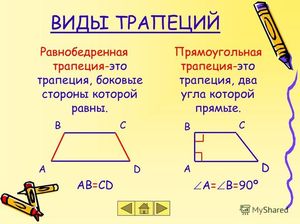
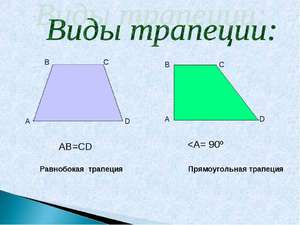
Различные виды указаны на рисунке ниже.

На изображении под номером 1 изображена произвольная трапеция. Номером 2 обозначен частный случай — прямоугольная трапеция, одна из сторон которой перпендикулярна её основаниям. Последняя фигура — тоже особый случай: это равнобедренная (равнобокая) трапеция, т. е. четырёхугольник с равными боковыми сторонами.

Важнейшие свойства и формулы

Для описания свойств четырёхугольника принято выделять определённые элементы. В качестве примера можно рассмотреть произвольную трапецию ABCD.

В её состав входят:

• основания BC и AD — две стороны, параллельные по отношению друг к другу;
• боковые стороны AB и CD — два непараллельных элемента;
• диагонали AC и BD — отрезки, соединяющие противоположные вершины фигуры;
• высота трапеции CH — перпендикулярный основаниям отрезок;
• средняя линия EF — линия, соединяющая середины боковых сторон.

Основные свойства элементов

Чтобы решить задачи по геометрии или доказать какие-либо утверждения, наиболее часто используют свойства, которые связывают различные элементы четырёхугольника. Они формулируются следующим образом:

1. Средняя линия всегда проходит параллельно обоим основаниям фигуры и численно равна их полусумме: EF = (BC + AD)/2.
2. Точка пересечения диагоналей фигуры разделяет их с таким же соотношением длины, с каким относятся основания трапеции: AD : BC = AO : CO = DO : BO.
3. Основание можно вычислить, зная длину второго основания и средней линии: BC = 2 · EF — AD, AD = 2 · EF — BC.
4. Боковые стороны вычисляются, если известна высота фигуры и синус угла при основании: AB = CH / sinA, CD = CH / sinD.
5. Для расчёта высоты необходимо знать, чему равна боковая сторона и прилегающий угол: CH = AB · sinA = CD · sinD.

Кроме того, часто полезно знать и применять следующие утверждения:

1. Биссектриса, проведённая из произвольного угла, отделяет на основании отрезок, длина которого равна боковой стороне фигуры.
2. При проведении диагоналей образуются 4 треугольника; из них 2 треугольника, образованных основаниями и отрезками диагоналей, обладают подобием, а оставшаяся пара имеет одинаковую площадь.
3. Через точку пересечения диагоналей O, середины оснований, а также точку, в которой пересекаются продолжения боковых сторон, можно провести прямую.

Вычисление периметра и площади

Периметр рассчитывается как сумма длин всех четырёх сторон (аналогично любой другой геометрической фигуре):

P = AD + BC + AB + CD.

Есть несколько способов, как можно рассчитать площадь трапеции по формуле. Следует выбрать из них наиболее подходящий вариант, опираясь на то, какие данные известны по условию задачи.

Вписанная и описанная окружность

Окружность возможно описать около трапеции только в том случае, когда боковые стороны четырёхугольника равны.

Чтобы вычислить радиус описанной окружности, необходимо знать длины диагонали, боковой стороны и большего основания. Величина p, используемая в формуле, рассчитывается как полусумма всех вышеперечисленных элементов: p = (a + c + d)/2.

Для вписанной окружности условие будет следующим: сумма оснований должна совпадать с суммой боковых сторон фигуры. Радиус её можно найти через высоту, и он будет равен r = h/2.

Частные случаи

Рассмотрим часто встречаемый случай — равнобокую (равностороннюю) трапецию. Её признаки — равенство боковых сторон или равенство противолежащих углов. К ней применимы все утверждения, которые характерны для произвольной трапеции. Другие свойства равнобедренной трапеции:

1. Прямая, которая проходит через середины оснований фигуры, пересекает их под углом 90 градусов.
2. Углы, лежащие при любых основаниях, попарно равны.
3. Длины диагоналей совпадают.
4. Высота будет равна средней линии, если диагонали проходят перпендикулярно друг к другу.
5. Высота, опущенная из вершины к основанию, делит его на 2 отрезка, длина большего вычисляется как половина суммы оснований, а длина меньшего — как половина разности.

Прямоугольная трапеция встречается в задачах не так часто. Её признаки — наличие двух смежных углов, равных 90 градусов, и наличие боковой стороны, перпендикулярной основаниям. Высота в таком четырёхугольнике одновременно является одной из его сторон.

Все рассмотренные свойства и формулы обычно используются для решения планиметрических задач. Однако также их приходится применять в некоторых задачах из курса стереометрии, например, при определении площади поверхности усечённой пирамиды, внешне напоминающей объёмную трапецию.