Определение логарифма и его свойства: теория и решение задач

По мере развития общества, усложнения производства развивалась и математика. Движение от простого к сложному. От обычного учёта методом сложения и вычитания, при их многократном повторении, пришли к понятию умножения и деления. Сокращение многократно повторяемой операции умножения стало понятием возведения в степень. Первые таблицы зависимости чисел от основания и числа возведения в степень были составлены ещё в VIII веке индийским математиком Варасена. С них и можно отсчитывать время возникновения логарифмов.

Оглавление:

• Исторический очерк
• Определение логарифма
• Разновидности логарифмов
• Правила и ограничения
• Как найти логарифм
• Уравнения и неравенства
• Практическое применение

Исторический очерк

Возрождение Европы в XVI веке стимулировало и развитие механики. Требовался большой объем вычисления, связанных с умножением и делением многозначных чисел. Древние таблицы оказали большую услугу. Они позволяли заменять сложные операции на более простые – сложение и вычитание. Большим шагом вперёд стала работа математика Михаэля Штифеля, опубликованная в 1544 году, в которой он реализовал идею многих математиков. Что позволило использовать таблицы не только для степеней в виде простых чисел, но и для произвольных рациональных.

В 1614 году шотландец Джон Непер, развивая эти идеи, впервые ввёл новый термин «логарифм числа». Были составлены новые сложные таблицы для расчёта логарифмов синусов и косинусов, а также тангенсов. Это сильно сократило труд астрономов.

Стали появляться новые таблицы, которые успешно использовались учёными на протяжении трёх веков. Прошло немало времени, прежде чем новая операция в алгебре приобрела свой законченный вид. Было дано определение логарифма, и его свойства были изучены.

Только в XX веке с появлением калькулятора и компьютера человечество отказалось от древних таблиц, успешно работавших на протяжении XIII веков.

Определение логарифма

Сегодня мы называем логарифмом b по основанию a число x, которое является степенью числа а, чтобы получилось число b. В виде формулы это записывается: x = log a(b).

Например, log 3(9) будет равен 2. Это очевидно, если следовать определению. Если 3 возвести в степень 2, то получим 9.

Так, сформулированное определение ставит только одно ограничение, числа a и b должны быть вещественными.

Разновидности логарифмов

Классическое определение носит название вещественный логарифм и фактически является решением уравнения a^x = b. Вариант a = 1 является пограничным и не представляет интереса. Внимание: 1 в любой степени равно 1.

Вещественное значение логарифма определено только при основании и аргументе больше 0, при этом основание не должно равняться 1.

Особое место в области математики играют логарифмы, которые будут называться в зависимости от величины их основания:

• Двоичные с основанием a = 2, нашли своё применение во многих разделах дискретной математики, информатике, а также теории информации; записываются как lb (b).
• Десятичные с основанием a = 10; записываются как lg (b).
• Натуральные с основанием a = e, где математическая константа e = 2,71828 - иррациональное и трансцендентное число, называемое Постоянная Эйлера; записываются как ln (b).

Правила и ограничения

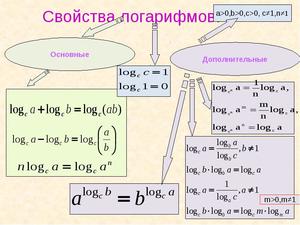
Основополагающим свойством логарифмов является правило: логарифм произведения равен логарифмической сумме. log abp = lоg a(b) + log a(p).

Как вариант этого утверждения будет: log с(b/p) = lоg с(b) - log с(p), функция частного равна разности функций.

Из предыдущих двух правил легко видно, что: lоg a(b^p) = p * log a(b).

Среди других свойств можно выделить:

• Правило тождественности, когда a^loga(b) = b, следствием этого правила является следующее утверждение: если a^loga(b) = a^loga(c), то b = c.
• Замечательные значения отражены в двух формулах: логарифм единицы всегда равен нулю log a(1) = 0 и логарифм числа, равного основанию, равен единице log a(a) = 1.
• При использовании отрицательных чисел можно применить формулу, справедливую для модуля чисел: log c|ab| = log c|a| + log c|b|.

Замечание. Не надо делать распространённую ошибку — логарифм суммы не равен сумме логарифмов.

Как найти логарифм

Многие века операция поиска логарифма была довольно трудоёмкой задачей. Математики пользовались известной формулой логарифмической теории разложения на многочлен:

ln (1 + x) = x - (x^2)/2 + (x^3)/3 - ( x^4)/4 + … + ((-1)^(n + 1))*((x^n)/n), где n — натуральное число больше 1, определяющее точность вычисления.

Логарифмы с другими основаниями вычислялись, используя теорему о переходе от одного основания к другому и свойстве логарифма произведения.

Так как этот способ очень трудоёмкий и при решении практических задач трудноосуществим, то использовали заранее составленные таблицы логарифмов, что значительно ускоряло всю работу.

В некоторых случаях использовали специально составленные графики логарифмов, что давало меньшую точность, но значительно ускоряло поиск нужного значения. Кривая функции y = log a(x), построенная по нескольким точкам, позволяет с помощью обычной линейки находить значения функции в любой другой точке. Инженеры длительное время для этих целей использовали так называемую миллиметровую бумагу.

В XVII веке появились первые вспомогательные аналоговые вычислительные условия, которые к XIX веку приобрели законченный вид. Наиболее удачное устройство получило название логарифмическая линейка. При всей простоте устройства, её появление значительно ускорило процесс всех инженерных расчётов, и это переоценить трудно. В настоящее время уже мало кто знаком с этим устройством.

Появление калькуляторов и компьютеров сделало бессмысленным использование любых других устройств.

Уравнения и неравенства

Для решения различных уравнений и неравенств с использованием логарифмов применяются следующие формулы:

• Переход от одного основания к другому: lоg a(b) = log c(b) / log c(a);
• Как следствие предыдущего варианта: lоg a(b) = 1 / log b(a).

Для решения неравенств полезно знать:

• Значение логарифма будет положительным только в том случае, когда основание и аргумент одновременно больше или меньше единицы; если хотя бы одно условие нарушено, значение логарифма будет отрицательным.
• Если функция логарифма применяется к правой и левой части неравенства, и основание логарифма больше единицы, то знак неравенства сохраняется; в противном случае он меняется.

Примеры задач

Рассмотрим несколько вариантов применения логарифмов и их свойства. Примеры с решением уравнений:

• Задача 1. Решить уравнение log 2(2x-1) = 4. Решение: по определению 2х - 1 = 2⁴ , или 2х - 1 = 16, далее 2х = 17, получаем х = 8,5. Ответ: при значении х = 8,5 уравнение действительно.
• Задача 2. Вычислить log 6(30) / log 30(6) - log 6(180) / log5(6). Решение: приведём к одному основанию 6. Следующим действием раскрываем скобки и вместо логарифма 6 по основанию 6 подставляем его значение 1. Таким образом, log 6(30) * lоg 6(30) - log 6(180) * log 6(5). Разложим числа на простые множители log 6(5*6) * log 6(5*6) - lоg 6(5*6*6) * log 6(5) и заменяем логарифм 5 по основанию 6 на t. Тогда (t +1) * (t +1) - (t +2) * t. Раскрываем скобки t² + t + t +1 - t ² - 2t. Приводим подобные члены и получаем 1. Ответ: значение выражения равно 1.

Рассмотрим вариант размещения логарифма в степени:

• Задача 3. Вычислить 25^log 5(3). Решение: в условиях задачи запись аналогична следующей (5^2)^log5(3) или 5^(2 * log 5(3)). Запишем по-другому: 5^log 5(3*2), или квадрат числа в качестве аргумента функции можно записать как квадрат самой функции (5^log 5(3))^2. Используя свойства логарифмов, это выражение равно 3^2. Ответ: в результате вычисления получаем 9.

Практическое применение

Являясь исключительно математическим инструментом, кажется далёким от реальной жизни, что логарифм неожиданно приобрёл большое значение для описания объектов реального мира. Трудно найти науку, где его не применяют. Это в полной мере относится не только к естественным, но и гуманитарным областям знаний.

Логарифмические зависимости

Приведём несколько примеров числовых зависимостей:

• Число простых чисел на интервале от 1 до n приблизительно равно n / ln (n).
• Для поиска k-го простого числа можно пользоваться формулой k * ln (k).
• Логарифмическое распределение часто используется для оценки вероятностных событий в генетике и физике.
• В информатике известно, что для хранения в памяти компьютера натурального числа N потребуется log 2(N) + 1 бит памяти.

Механика и физика

Исторически механика и физика всегда развивались с использованием математических методов исследования и одновременно служили стимулом для развития математики, в том числе логарифмов. Теория большинства законов физики написана языком математики. Приведём только два примера описания физических законов с использованием логарифма.

Решать задачу расчёта такой сложной величины как скорость ракеты можно, применяя формулу Циолковского, которая положила начало теории освоения космоса:

V = I * ln (M1/M2), где

• V – конечная скорость летательного аппарата.
• I – удельный импульс двигателя.
• M 1 – начальная масса ракеты.
• M 2 – конечная масса.

Другой важный пример — это использование в формуле другого великого учёного Макса Планка, которая служит для оценки равновесного состояния в термодинамике.

S = k * ln (Ω), где

• S – термодинамическое свойство.
• k – постоянная Больцмана.
• Ω – статистический вес разных состояний.

Химия

Менее очевидным будет использования формул в химии, содержащих отношение логарифмов. Приведём тоже только два примера:

• Уравнение Нернста, условие окислительно-восстановительного потенциала среды по отношению к активности веществ и константой равновесия.
• Расчёт таких констант, как показатель автопролиза и кислотность раствора тоже не обходятся без нашей функции.

Психология и биология

И уж совсем непонятно при чём здесь психология. Оказывается, сила ощущения хорошо описывается этой функцией как обратное отношение значения интенсивности раздражителя к нижнему значению интенсивности.

После вышеприведённых примеров уже не удивляет, что и в биологии широко используется тема логарифмов. Про биологические формы, соответствующие логарифмическим спиралям, можно писать целые тома.

Другие области

Кажется, невозможно существование мира без связи с этой функцией, и она правит всеми законами. Особенно, когда законы природы связаны с геометрической прогрессией. Стоит обратиться к сайту МатПрофи, и таких примеров найдётся множество в следующих сферах деятельности:

• Теории акустики.
• Радиотехнике и электросвязи.
• Астрономии.
• Сейсмологии.
• Оптике.
• Фотографии.
• Сельском хозяйстве.
• Теории управления.

Список может быть бесконечным. Освоив основные закономерности этой функции, можно окунуться в мир бесконечной мудрости.